题目内容
8.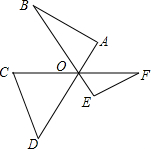 已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.
已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.
分析 分别得到△AOP≌△AOB、△PGQ≌△EOF、△QOD≌△COD,从而得到S△AOP=S△AOB,S△PGQ=S△EOF,S△QOD=S△COD,从而利用S△OAB+S△OCD+S△OEF=S△AOP+S△PGQ+S△QOD求解.
解答 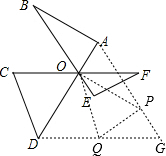 证明:作AG∥BE,DG∥CF,
证明:作AG∥BE,DG∥CF,
则∠DAG=∠AOB=60°=∠COD=∠ADG,
∴△ADG是等边三角形且边长为2,
∴S△ADG=$\frac{\sqrt{3}}{4}$×22=$\sqrt{3}$,
在AG上截取AP=OB,连接OP,
则△AOP≌△AOB,
即S△AOP=S△AOB,
∵BE=AG,OB=AP,
∴OE=PG,
在DG上截取GQ=OF,连接PQ,
则△PGQ≌△EOF,
即:S△PGQ=S△EOF,
∵GD=CF,GQ=OF,
∴DQ=OC,
∴△QOD≌△COD,即S△QOD=S△COD,
∴S△OAB+S△OCD+S△OEF=S△AOP+S△PGQ+S△QOD=S△ADG-S△OPQ=$\sqrt{3}$-S△OPQ<$\sqrt{3}$.
点评 本题考查了面积及等积变换的知识,解题的关键是正确的作出辅助线,构造全等的三角形,难度偏大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
则y关于x的关系式为y=0.5x+10.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
 如图,以△ABC的边AB,AC为边向外作等边△ABE和△ACD,连接BD,CE,求证:BD=CE.
如图,以△ABC的边AB,AC为边向外作等边△ABE和△ACD,连接BD,CE,求证:BD=CE.




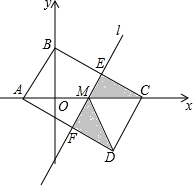 如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值.
如图,在平面直角坐标系中A(-2,0),B(0,3),C(6,0),D(4,-3),M(2,0),直线l过M点,若S四边形ABCD=mS阴影,求m的值.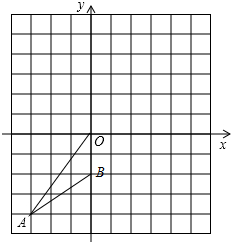 如图,已知,在平面直角坐标系中,A(-3,-4),B(0,-2).
如图,已知,在平面直角坐标系中,A(-3,-4),B(0,-2).