题目内容
19. 如图,以△ABC的边AB,AC为边向外作等边△ABE和△ACD,连接BD,CE,求证:BD=CE.
如图,以△ABC的边AB,AC为边向外作等边△ABE和△ACD,连接BD,CE,求证:BD=CE.
分析 根据等边三角形的性质得到AE=AB,AD=AC,∠EAB=∠DAC=60°,则∠BAD=∠EAC,再根据三角形全等的判定方法可证得△ACE≌△ADB,然后根据全等的性质即可得到结论.
解答 证明:∵△ABE和△ACD是等边三角形,
∴AE=AB,AD=AC,∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠CAB,
∴∠BAD=∠EAC,
在△ACE和△ADB中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠DAB}\\{AC=AD}\end{array}\right.$,
∴△ACE≌△ADB(SAS),
∴BD=CE.
点评 本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角也相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等边三角形的性质.

练习册系列答案
相关题目
11.下列计算中,正确的是( )
| A. | (x4)3=x12 | B. | a2a5=a10 | C. | (3a)2=6a2 | D. | a6÷a2=a3 |
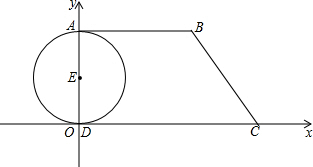 如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
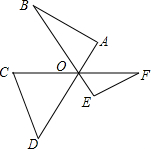 已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.
已知线段OA,OB,OC,OD,OE,OF,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=60°,且AD=BE=CF=2,求证:S△OAB+S△OCD+S△OEF<$\sqrt{3}$.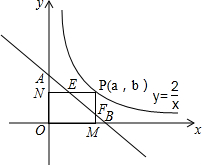 如图,已知P(a,b)在反比例函数y=$\frac{2}{x}$的图象上,直线y=kx+1-k与坐标轴交于A、B两点,∠ABO=45°,过点P分别作两坐标轴的垂线PM、PN,垂足分别为M、N.
如图,已知P(a,b)在反比例函数y=$\frac{2}{x}$的图象上,直线y=kx+1-k与坐标轴交于A、B两点,∠ABO=45°,过点P分别作两坐标轴的垂线PM、PN,垂足分别为M、N.