题目内容
7.(1)解不等式$\frac{x-1}{3}$≤5-x,并把解集表示在数轴上.(2)解不等式组$\left\{\begin{array}{l}{\frac{1+3x}{2}-x<1}\\{5x-12≤2(4x-3)}\end{array}\right.$并把解集表示在数轴上.
分析 (1)先求出不等式的解集,再在数轴上表示出来即可.
(2)分别解出不等式,进而在数轴上表示出解集.
解答 解:(1)去分母得,x-1≤3(5-x),
去括号得,x-1≤15-3x,
移项得,x+3x≤15+1,
合并同类项得,4x≤16,
系数化为1得,x≤4.
在数轴上表示为: .
.
(2)$\left\{\begin{array}{l}{\frac{1+3x}{2}-x<1①}\\{5x-12≤2(4x-3)②}\end{array}\right.$,
解①得:x<1,
解②得:x≥-2,
故不等式的解集为:-2≤x<1,
在数轴上表示如图: .
.
点评 此题考查了一元一次不等式组的解法,其中一元一次不等式的解法步骤为:去分母,去括号,移项,合并同类项,将x系数化为1,不等式组取解集的方法为:同大取大;同小取小;大小小大去中间;大大小小无解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.把方程$\frac{0.2x-1}{0.3}$-2=$\frac{0.1x-0.7}{0.5}$的分母化为整数的方程是( )
| A. | $\frac{2x-10}{3}$-20=$\frac{x-7}{5}$ | B. | $\frac{2x-10}{3}$-2=$\frac{x-7}{5}$ | C. | $\frac{2x-1}{3}$-2=$\frac{x-7}{5}$ | D. | $\frac{2x-1}{3}$-20=$\frac{x-7}{5}$ |
16.以$\frac{1+\sqrt{3}}{2}$和$\frac{-1+\sqrt{3}}{2}$为根的一个一元二次方程是( )
| A. | x2-$\sqrt{3}$x+$\frac{1}{2}$=0 | B. | x2+$\sqrt{3}$x+$\frac{1}{2}$=0 | C. | x2-$\sqrt{3}$x+1=0 | D. | x2+$\sqrt{3}$x-$\frac{1}{2}$=0 |
 (1)完成下面的证明.
(1)完成下面的证明.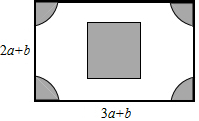 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.