题目内容
 在平面直角坐标系系xOy中,直线y=2x+m与y轴交于点A,与直线y=-x+4交于点B(3,n),P为直线y=-x+4上一点.
在平面直角坐标系系xOy中,直线y=2x+m与y轴交于点A,与直线y=-x+4交于点B(3,n),P为直线y=-x+4上一点.(1)求m,n的值;
(2)当线段AP最短时,求点P的坐标.
考点:一次函数图象上点的坐标特征,垂线段最短
专题:
分析:(1)首先把点B(3,n)代入直线y=-x+4得出n的值,再进一步代入直线y=2x+m求得m的值即可;
(2)过点A作直y=-x+4的垂线,垂足为P,进一步利用等腰直角三角形的性质和(1)中与y轴交点的坐标特征解决问题.
(2)过点A作直y=-x+4的垂线,垂足为P,进一步利用等腰直角三角形的性质和(1)中与y轴交点的坐标特征解决问题.
解答: 解:(1)∵点B(3,n)在直线上y=-x+4,
解:(1)∵点B(3,n)在直线上y=-x+4,
∴n=1,B(3,1)
∵点B(3,1)在直线上y=2x+m上,
∴m=-5.
(2)过点A作直线y=-x+4的垂线,垂足为P,
此时线段AP最短.
∴∠APN=90°,
∵直线y=-x+4与y轴交点N(0,4),直线y=2x-5与y轴交点A(0,5),
∴AN=9,∠ANP=45°,
∴AM=PM=
,
∴OM=
∴P(
,-
).
 解:(1)∵点B(3,n)在直线上y=-x+4,
解:(1)∵点B(3,n)在直线上y=-x+4,∴n=1,B(3,1)
∵点B(3,1)在直线上y=2x+m上,
∴m=-5.
(2)过点A作直线y=-x+4的垂线,垂足为P,
此时线段AP最短.
∴∠APN=90°,
∵直线y=-x+4与y轴交点N(0,4),直线y=2x-5与y轴交点A(0,5),
∴AN=9,∠ANP=45°,
∴AM=PM=
| 9 |
| 2 |
∴OM=
| 1 |
| 2 |
∴P(
| 9 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征与垂线段最短的性质,结合图形,选择适当的方法解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,直线AB与反比例函数图象相交于A、B两点,已知A(1,4),连接OA、OB,当△AOB的面积为
如图所示,直线AB与反比例函数图象相交于A、B两点,已知A(1,4),连接OA、OB,当△AOB的面积为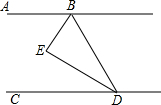 如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°. 为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住.
为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.