题目内容
20.化简:(1)(x+y)(x-2y)-(x-2y)2
(2)($\frac{{x}^{2}}{x+2}$-x+2)÷$\frac{{x}^{3}-{2x}^{2}}{4{-x}^{2}}$.
分析 (1)根据整式乘法法则即可求出答案.
(2)先将分式的分子与分母进行因式分解,然后利用分式的基本性质即可求出答案.
解答 解:(1)原式=x2-2xy+xy-2y2-(x2-4xy+4y2)
=x2-2xy+xy-2y2-x2+4xy-4y2
=3xy-6y2
(2)原式=($\frac{{x}^{2}}{x+2}$-x+2)÷$\frac{{x}^{2}(x-2)}{(2-x)(2+x)}$
=($\frac{{x}^{2}}{x+2}$-x+2)÷$\frac{-{x}^{2}}{x+2}$
=-($\frac{{x}^{2}}{x+2}$-x+2)×$\frac{x+2}{{x}^{2}}$
=-[1-$\frac{(x-2)(x+2)}{{x}^{2}}$]
=-$\frac{4}{{x}^{2}}$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.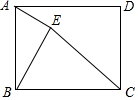 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )| A. | $\frac{3}{2}$ | B. | 2$\sqrt{10}$-2 | C. | 2$\sqrt{13}$-2 | D. | 4 |
10.用科学记数法表示2017(保留三个有效数字),下列说法正确的是( )
| A. | 0.20×104 | B. | 2.02×103 | C. | 2.0×104 | D. | 2.01×103 |

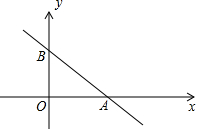 如图,直线y=-$\frac{3}{4}$x+3与坐标轴分别交于点A、B.
如图,直线y=-$\frac{3}{4}$x+3与坐标轴分别交于点A、B.