题目内容
15.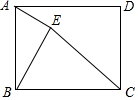 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )| A. | $\frac{3}{2}$ | B. | 2$\sqrt{10}$-2 | C. | 2$\sqrt{13}$-2 | D. | 4 |
分析 由AE⊥BE知点E在以AB为直径的半⊙O上,连接CO交⊙O于点E′,当点E位于点E′位置时,线段CE取得最小值,利用勾股定理可得答案.
解答 解:如图,
∵AE⊥BE,
∴点E在以AB为直径的半⊙O上,
连接CO交⊙O于点E′,
∴当点E位于点E′位置时,线段CE取得最小值,
∵AB=4,
∴OA=OB=OE′=2,
∵BC=6,
∴OC=$\sqrt{B{C}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
则CE′=OC-OE′=2$\sqrt{10}$-2,
故选:B.
点评 本题主要考查圆周角定理、圆的基本性质及矩形的性质、勾股定理,根据AE⊥BE知点E在以AB为直径的半⊙O上是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
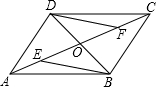 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF,求证:BE=DF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF,求证:BE=DF.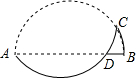 如图,半圆形纸片的直径AB=10,AC是弦,∠BAC=15°,将半圆形纸片沿AC折叠,弧$\widehat{AC}$交直径AB于点D,则线段AD的长为5$\sqrt{3}$.
如图,半圆形纸片的直径AB=10,AC是弦,∠BAC=15°,将半圆形纸片沿AC折叠,弧$\widehat{AC}$交直径AB于点D,则线段AD的长为5$\sqrt{3}$.