题目内容
3. 如图,矩形纸片ABCD的边AD=9,AB=3,将其沿EF折叠,使点D与点B重合,则折痕EF的长为( )
如图,矩形纸片ABCD的边AD=9,AB=3,将其沿EF折叠,使点D与点B重合,则折痕EF的长为( )| A. | $\frac{10}{3}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{3}$ | D. | 4 |
分析 作FM⊥AD于M,则∠FME=90°,FM=AB=3,由折叠的性质得出BE=DE,∠BEF=∠DEF,再求出BF=BE,设AE=x,则BE=DE=9-x,根据勾股定理得出方程,解方程求出AE,得出DE、BF、EM,根据勾股定理求出EF即可.
解答 解:作FM⊥AD于M,如图所示: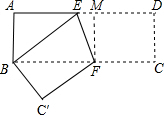
则∠FME=90°,FM=AB=3,
根据题意得:BE=DE,∠BEF=∠DEF,
∵四边形ABCD是矩形,
∴∠A=90°,AD∥BC,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BF=BE,
设AE=x,则BE=DE=BF=9-x,
根据勾股定理得:
AB2+AE2=BE2,即32+x2=(9-x)2,
解得:x=4,
∴AE=4,
∴DE=BF=5,
∴CF=DM=4,
∴EM=1,
根据勾股定理得:EF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
故选:B.
点评 本题考查了翻折变换的性质、矩形的性质、勾股定理、等腰三角形的判定;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
13.△ABC与△A′B′C′是位似图形,且△ABC与△A′BC′的位似比是2:3,那么这两个相似三角形面积的比是( )
| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 4:9 | D. | 8:27 |
14.某工厂现在平均每天比原计划多生产10台机器,现在生产700台机器所需时间与原计划生产500台机器所需时间相同,设原计划平均每天生产x台机器,根据题意列方程得( )
| A. | $\frac{700}{x}$=$\frac{500}{x+10}$ | B. | $\frac{700}{x-10}$=$\frac{500}{x}$ | C. | $\frac{700}{x}$=$\frac{500}{x-10}$ | D. | $\frac{700}{x+10}$=$\frac{500}{x}$ |
11.某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3,每立方米收费2元;若用水超过20m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )m3.
| A. | 38 | B. | 34 | C. | 28 | D. | 44 |
18.学校举行广播操比赛,八年级三个班的各项得分及三项得分的平均数如下(单位:分).
根据表中信息回答下列问题:
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
| 服装统一 | 进退场有序 | 动作规范 | 动作整齐 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
8.下列说法中正确的是( )
| A. | 无理数是无限不循环小数 | B. | 无限小数都是无理数 | ||
| C. | -1的平方根是±1 | D. | -3是9的算术平方根 |
13.某事件发生的概率为$\frac{1}{4}$,则下列说法不正确的是( )
| A. | 无数次实验后,该事件发生的频率逐渐稳定在$\frac{1}{4}$左右 | |
| B. | 无数次实验中,该事件平均每4次出现1次 | |
| C. | 每做4次实验,该事件就发生1次 | |
| D. | 逐渐增加实验次数,该事件发生的频率就和$\frac{1}{4}$逐渐接近 |
 如图,一个表面涂满颜色的正方体,现将每条棱三等分,再把它切开变成若干个小正方体,两面都涂色的有12个.
如图,一个表面涂满颜色的正方体,现将每条棱三等分,再把它切开变成若干个小正方体,两面都涂色的有12个.