题目内容
13．某事件发生的概率为$\frac{1}{4}$，则下列说法不正确的是（ ）| A． | 无数次实验后，该事件发生的频率逐渐稳定在$\frac{1}{4}$左右 | |
| B． | 无数次实验中，该事件平均每4次出现1次 | |
| C． | 每做4次实验，该事件就发生1次 | |
| D． | 逐渐增加实验次数，该事件发生的频率就和$\frac{1}{4}$逐渐接近 |
分析 利用概率的意义分别判断后即可确定正确的选项．
解答 解：A、无数次实验后，该事件发生的频率逐渐稳定在$\frac{1}{4}$左右，正确，不符合题意；
B、无数次实验中，该事件平均每4次出现1次，正确，不符合题意；
C、每做4次试验，该事件可能发生一次，也可能发生两次，也有可能不发生，故错误，符合题意；
D、逐渐增加实验次数，该事件发生的频率就和$\frac{1}{4}$逐渐接近，正确，不符合题意，
故选C．
点评 本题考查了利用频率估计概率的知识，解题的关键是了解概率的意义，某事件发生的概率为$\frac{1}{4}$，不一定试验4次就一定有一次发生，难度不大．
练习册系列答案
相关题目
3．
如图，矩形纸片ABCD的边AD=9，AB=3，将其沿EF折叠，使点D与点B重合，则折痕EF的长为（ ）
如图，矩形纸片ABCD的边AD=9，AB=3，将其沿EF折叠，使点D与点B重合，则折痕EF的长为（ ）| A． | $\frac{10}{3}$ | B． | $\sqrt{10}$ | C． | 2$\sqrt{3}$ | D． | 4 |
8．用配方法解方程2y2+3=7y，配方后得（ ）
| A． | （y+$\frac{7}{4}$）2=$\frac{25}{16}$ | B． | （y-$\frac{7}{4}$）2=$\frac{25}{16}$ | C． | （y+$\frac{7}{2}$）2=$\frac{25}{16}$ | D． | （y-$\frac{7}{2}$）2=$\frac{25}{16}$ |
5．计算-$\frac{b}{a}+\frac{b+5}{a}$的结果正确的是（ ）
| A． | $-\frac{5}{a}$ | B． | $\frac{5}{a}$ | C． | $-\frac{2b+5}{a}$ | D． | $\frac{-2b+5}{a}$ |
2．下列事件中是必然事件的是（ ）
| A． | 任意掷一枚硬币，落地后正面和反面同时朝上 | |
| B． | 李阿姨申请了北京市小客车购买指标，在申请后的第一次“摇号”时就中签 | |
| C． | 分别从写有2、4、5三个数字的三张卡片中随机抽出一张，卡片上的数字一定能被2整除 | |
| D． | 哥哥的年龄比弟弟大． |
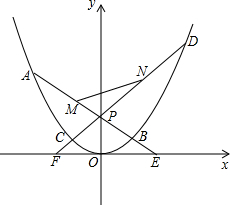抛物线C0的顶点为原点O，且过点G（2，1）．如图，过点P（0，2）分别作两条直线，l1：y=k1x+2和l2：y=k2x+2（其中k1•k2≠0），两直线分别与抛物线、x轴相交于点A、B、E和D、C、F，且M、N分别是AB、CD的中点．