如图.五边形ABCDE中.AB∥CD.∠1+∠2+∠3等于( )A．90°B．180°C．210°D．270° 题目和参考答案——青夏教育精英家教网—

题目内容

1．

如图，五边形ABCDE中，AB∥CD，∠1+∠2+∠3等于（　　）

A．

90°

B．

180°

C．

210°

D．

270°

分析根据两直线平行，同旁内角互补求出∠B+∠C=180°，从而得到以点B、点C为顶点的五边形的两个外角的度数之和等于180°，再根据多边形的外角和定理列式计算即可得解．

解答解：∵AB∥CD，
∴∠B+∠C=180°，
∴∠4+∠5=180°，
根据多边形的外角和定理，∠1+∠2+∠3+∠4+∠5=360°，
∴∠1+∠2+∠3=360°-180°=180°．
故选：B．

点评本题考查了平行线的性质，多边形的外角和定理，是基础题，明确多边形的外角和为360°是解题的关键．

练习册系列答案

相关题目

11．解方程．
（1）3x²-x-4=0
（2）（x-1）²=4（x-5）²．

12．在?ABCD中，若∠A+∠C=160°，则∠C的度数为80°．

9．

如图，在梯形ABCD中，AD∥BC，∠ADC=135°，AB+BC=24，AB⊥BC，梯形ABCD的面积为42m²，求AB、BC的大小．

16．（1）分解因式：3x²-27
（2）计算：（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$-$\frac{x+4}{x-2}$）÷$\frac{x+4}{x-2}$．

6．下列分式中，为最简分式的是（　　）

A．

$\frac{a+3}{{a}^{2}+3}$

B．

$\frac{a+b}{{a}^{2}-{b}^{2}}$

13．

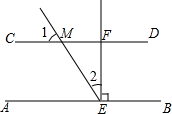如图，AB∥CD，EF⊥AB与E，EF交CD于F，FM交CD于M，已知∠1=55°，则∠MEB等于（　　）

	A．	过一点有且只有一条直线与已知直线垂直
	B．	过一点有且只有一条直线与已知直线平行
	C．	垂直于同一直线的两条直线平行
	D．	平行于同一直线的两条直线平行

11．已知a，b，c为有理数，且a＜b，则下列不等式中正确的是（　　）

A．

$\frac{a}{c}$＜$\frac{b}{c}$

试题分类