题目内容
16.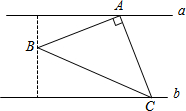 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,点B到a、b的距离分别为1和2,则△ABC的面积为5.
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,点B到a、b的距离分别为1和2,则△ABC的面积为5.
分析 作CD⊥a,再利用AAS证明△ABE与△ACD全等,利用全等三角形的性质解答即可.
解答 解:作CD⊥a,如图: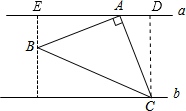 ,
,
∵∠BAC=∠ADC=∠BEA=90°,
∴∠EAB+∠EBA=∠DAC+∠EAB=90°,
∴∠EBA=∠DAC,
在△ABE与△ACD中,
$\left\{\begin{array}{l}{∠ABE=∠DAC}\\{∠BEA=∠ADC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD(AAS),
∴AE=CD=1+2=3,
∵BE=1,
∴AB=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,
∴△ABC的面积=$\frac{1}{2}AB•AC=\frac{1}{2}×\sqrt{10}×\sqrt{10}$=5,
故答案为:5.
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.

练习册系列答案
相关题目

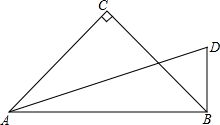 如图,已知AD=3,BD=1,AC=BC,∠C=∠ABD=90°,则BC=$\sqrt{5}$.
如图,已知AD=3,BD=1,AC=BC,∠C=∠ABD=90°,则BC=$\sqrt{5}$.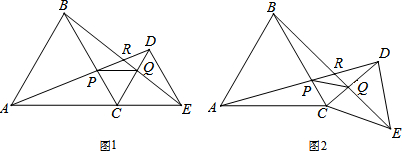

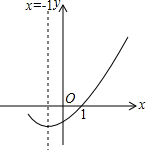 如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题: