题目内容
9. 如图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.
如图,已知A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE.(1)若∠AOB=35°,求∠DOE;
(2)试求∠BOD的度数.
分析 (1)利用角平分线的定义和平角的定义得到∠AOB+∠EOD=90°,则易得∠DOE的度数;
(2)利用角平分线的定义和平角的定义得到∠COB+∠COD=90°,则易得∠BOD的度数.
解答  解:(1)如图,∵A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,
解:(1)如图,∵A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,
∴∠AOB=$\frac{1}{2}$∠AOC,∠EOD=$\frac{1}{2}$∠COE,
∴∠AOB+∠EOD=$\frac{1}{2}$(∠AOC+∠COE)=90°.
又∵∠AOB=35°,
∴∠DOE=55°;
(2)如图,∵A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,
∴∠COB=$\frac{1}{2}$∠AOC,∠COD=$\frac{1}{2}$∠COE,
∴∠COB+∠COD=$\frac{1}{2}$(∠AOC+∠COE)=90°.
即∠BOD=90°.
点评 本题考查的是垂线的性质及角平分线的定义,熟知角平分线的定义是解答此题的关键.

练习册系列答案
相关题目
19.若把分式$\frac{x+3y}{2xy}$的x、y同时扩大10倍,则分式的值( )
| A. | 扩大为原来的10倍 | B. | 缩小为原来的$\frac{1}{10}$ | ||
| C. | 不变 | D. | 缩小为原来的$\frac{1}{5}$ |
17.一直角三角形的斜边长为13,其中一条直角边长为12,则另一直角边长为( )
| A. | 13 | B. | 12 | C. | 4 | D. | 5 |
4.“水是生命之源”,市自来水公司为鼓励用户节约用水,按以下规定收取水费:
(1)某用户1月份共用水70吨,问1月份应交水费多少元?
(2)若该用户2月份共交水费65元,问该用户2月份用水多少吨?
| 用水量/月 | 单位(元/吨) |
| 不超过40吨的部分 | 1 |
| 超过40吨的部分 | 1.5 |
| 另:每吨用水加收0.2元的城市污水处理费 | |
(2)若该用户2月份共交水费65元,问该用户2月份用水多少吨?
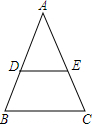 已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.
已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.


 ,那么在长方形框中,左下角与右上角两数之积减去左上角与右下角两数之积的差是多少?
,那么在长方形框中,左下角与右上角两数之积减去左上角与右下角两数之积的差是多少?