题目内容
12. 如图,⊙O是△ABC的外接圆,点D在⊙O上,已知∠ACB=∠D,BC=3,则AB的长是3.
如图,⊙O是△ABC的外接圆,点D在⊙O上,已知∠ACB=∠D,BC=3,则AB的长是3.
分析 由圆周角定理,可得∠ACB=∠D,又由∠ACB=∠D,可证得△ABC是等腰三角形,继而求得答案.
解答 解:∵∠A=∠D,∠ACB=∠D,
∴∠ACB=∠A,
∴AB=BC=3.
故答案为:3.
点评 此题考查了圆周角定理以及等腰三角形的判定.注意证得△ABC是等腰三角形是解此题的关键.

练习册系列答案
相关题目
7.下列变形属于移项的是( )
| A. | 由$\frac{x}{5}$=1,得x=5 | B. | 由-7x=2,得x=-$\frac{2}{7}$ | ||
| C. | 由-5x-2=0,得-2=5x | D. | 由-3+2x=9,得2x-3=9 |
17.一直角三角形的斜边长为13,其中一条直角边长为12,则另一直角边长为( )
| A. | 13 | B. | 12 | C. | 4 | D. | 5 |
4.“水是生命之源”,市自来水公司为鼓励用户节约用水,按以下规定收取水费:
(1)某用户1月份共用水70吨,问1月份应交水费多少元?
(2)若该用户2月份共交水费65元,问该用户2月份用水多少吨?
| 用水量/月 | 单位(元/吨) |
| 不超过40吨的部分 | 1 |
| 超过40吨的部分 | 1.5 |
| 另:每吨用水加收0.2元的城市污水处理费 | |
(2)若该用户2月份共交水费65元,问该用户2月份用水多少吨?
2.如果一个角的度数为20°16′,那么它的余角的度数为( )
| A. | 159°44′ | B. | 69°16′ | C. | 70°54′ | D. | 69°44′ |
 如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.
如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.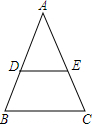 已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.
已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.