题目内容
如图，已知D、E分别是△ABC的边AB、AC上的点，G、F是BC上的点，且四边形DGFE是正方形，| AD |
| DB |
| 2 |
| 3 |
考点：相似三角形的判定与性质,正方形的性质
专题：
分析：设正方形的边长为x，再根据相似三角形的判定定理得出△ADE∽△ABC，求出x的值，进而可得出结论．
解答：解：设正方形的边长为x，
∵四边形DGFE是正方形，AH⊥BC，
∴AH⊥DE，△ADE∽△ABC，
∵AH=5cm，NH=xcm，
∴AN=5-x，
∴
=
=
，
∵
=
，
∴
=
，
∴
=
=
，
解得x=2，
BC=
，
∴S△ABC=
BC•AH=
×
×5=
，
S正方形DGFE=x2=4．
∵四边形DGFE是正方形，AH⊥BC，
∴AH⊥DE，△ADE∽△ABC，
∵AH=5cm，NH=xcm，
∴AN=5-x，
∴
| AN |
| AH |
| AD |
| AB |
| DE |
| BC |
∵
| AD |
| DB |
| 2 |
| 3 |
∴
| AD |
| AB |
| 3 |
| 5 |
∴
| 5-x |
| 5 |
| 3 |
| 5 |
| x |
| BC |
解得x=2，
BC=
| 10 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 25 |
| 3 |
S正方形DGFE=x2=4．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
下列不等式组无解的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
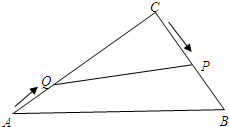已知：如图，在△ABC中，∠C=Rt∠，AB=10cm，BC=6cm，点P从点C开始沿边CB以2cm/s的速度向点B移动，与此同时，点Q从点A开始沿边AC以1cm/s的速度向点C移动，两点同时出发，当其中一点到达终点时，另一点也随之停止移动．若设移动时间为t秒．
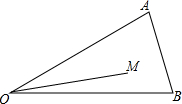如图，M是△AOB内一点，已知∠AOB=30°，OM=2，试在OA上确定一点E，在OB上确定一点F，使△MEF的周长最小，并求出△MEF周长的最小值．