题目内容
已知,在菱形ABCD中,E、F、G、H分别为各边的中点,求证:E、F、G、H四点在同一个圆上.
考点:四点共圆,直角三角形斜边上的中线,菱形的性质
专题:证明题
分析:根据菱形的性质可得∠AOD=90°,根据直角三角形斜边上的中线等于斜边的一半可得OH=
AD.同理可得:OE=
AB,OF=
BC,OG=
CD.然后根据菱形的性质可得AD=AB=BC=CD,从而有OH=OE=OF=OG,即可证到E、F、G、H四点在同一个圆上.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: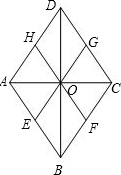 证明:如图.
证明:如图.
∵四边形ABCD是菱形,
∴AC⊥BD即∠AOD=90°.
∵H是AD的中点,
∴OH=
AD.
同理:OE=
AB,OF=
BC,OG=
CD.
∵四边形ABCD是菱形,
∴AD=AB=BC=CD,
∴OH=OE=OF=OG.
∴E、F、G、H四点在以点O为圆心,OH为半径的圆上,
即E、F、G、H四点在同一个圆上.
 证明:如图.
证明:如图.∵四边形ABCD是菱形,
∴AC⊥BD即∠AOD=90°.
∵H是AD的中点,
∴OH=
| 1 |
| 2 |
同理:OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵四边形ABCD是菱形,
∴AD=AB=BC=CD,
∴OH=OE=OF=OG.
∴E、F、G、H四点在以点O为圆心,OH为半径的圆上,
即E、F、G、H四点在同一个圆上.
点评:本题考查了菱形的性质、直角三角形斜边上的中线等于斜边的一半、四点共圆的判定等知识,本题中要证明四点共圆,找到圆心是关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
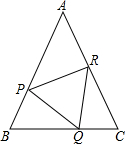 如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR.
如图,在△ABC中,AB=AC,P、Q、R分别在AB、AC上,且BP=CQ,BQ=CR. (用反证法证明)已知直线a∥c,b∥c,求证:a∥b.
(用反证法证明)已知直线a∥c,b∥c,求证:a∥b. 如图,已知D、E分别是△ABC的边AB、AC上的点,G、F是BC上的点,且四边形DGFE是正方形,
如图,已知D、E分别是△ABC的边AB、AC上的点,G、F是BC上的点,且四边形DGFE是正方形,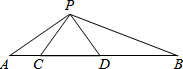 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.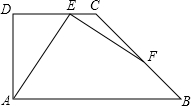 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AD=CD=4,∠B=45°,点E为直线DC上一点,连接AE,作EF⊥AE交直线CD于点F.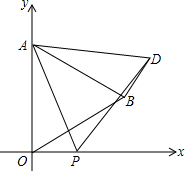 在平面直角坐标系中,已知点O为坐标原点,点A(0,4).在y轴右侧作等边△AOB,点B在第一象限.点P是x轴上的一个动点,连接AP,在右侧作等边△ADP,当四边形AODB是梯形时,求点P的坐标.
在平面直角坐标系中,已知点O为坐标原点,点A(0,4).在y轴右侧作等边△AOB,点B在第一象限.点P是x轴上的一个动点,连接AP,在右侧作等边△ADP,当四边形AODB是梯形时,求点P的坐标.