题目内容
11.求证:有无穷多个n,能使多项式n2+3n+7;(1)表示合数;
(2)是11的倍数.
分析 (1)先把原式化为n(n+3)+7的形式,再设n=7k或n=7k-3,代入代数式即可得到关于k的式子,由合数的定义即可解答;
(2)设n2+3n+7=11k,(k是正整数),再把方程左边因式分解,由合数的定义即可解答.
解答 证明:(1)要使n(n+3)+7是合数.
则只要n(n+3)是7的倍数就可以.
要使n(n+3)是7的倍数,则n=7k或n=7k-3,
当n=7k(k为自然数)时,原式=49k2+21k+7=7(7k2+3k+1),
同理,当n=7k-3时,原式=49k2-21k+7=7(7k2-3k+1),
满足此条件的自然数k有无数个,所以对应的n也有无穷多个;
(2)使多项式n2+3n+7为11的倍数,
设n2+3n+7=11k(k是正整数),
n2+3n-4=11(k-1),
(n+4)(n-1)=11(k-1),
要使n2+3n+7是11的倍数,
则只要(n+4)(n-1)是11的倍数就可以.
则n=11k-4或n=11k+1(k=0、1、2、3…),
当n=11k-4时,原式=11k(11k-5)+11=11(11k2-5k+1),
同理可得,当n=11k+1时,原式=11k(11k+5)+11=11(11k2+5k+1),
满足此条件的k有无穷多个,
故表示为11的倍数的n也有无穷多个.
点评 本题考查的是质数与合数,熟知合数的定义是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.函数y=$\frac{k}{x}$的图象经过点(-2,4),则下列四个点在y=$\frac{k}{x}$图象上的是( )
| A. | (4,-2) | B. | (2,4) | C. | (1,8) | D. | (-2,-4) |
1.下列运算正确的是( )
| A. | (x2)3+(x3)2=2x6 | B. | (x2)3•(x2)3=2x12 | C. | x4•(2x)2=2x6 | D. | (2x)3•(-x)2=-8x5 |
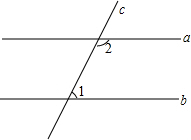 如图,直线a,b被直线c所截,且a∥b,∠1=40°,则∠2=140度.
如图,直线a,b被直线c所截,且a∥b,∠1=40°,则∠2=140度.