题目内容
2．先化简（1-$\frac{1}{x-1}$）÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$，再从-2，-1，0中选一个合适的数代入并求值．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x=0代入计算即可求出值．
解答 解：原式=$\frac{x-2}{x-1}$•$\frac{（x+1）（x-1）}{（x-2）^{2}}$
=$\frac{x+1}{x-2}$，
当x=0时，原式=-$\frac{1}{2}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
17．
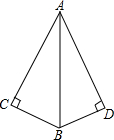如图所示，∠C=∠D=90°添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．
以下给出的条件适合的是（ ）
如图所示，∠C=∠D=90°添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是（ ）
| A． | AC=AD | B． | AB=AB | C． | ∠ABC=∠ABD | D． | ∠BAC=∠BAD |
7．
在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是（ ）
在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是（ ）| A． | （4n-1，$\sqrt{3}$） | B． | （2n-1，$\sqrt{3}$） | C． | （4n+1，$\sqrt{3}$） | D． | （2n+1，$\sqrt{3}$） |
