��Ŀ����
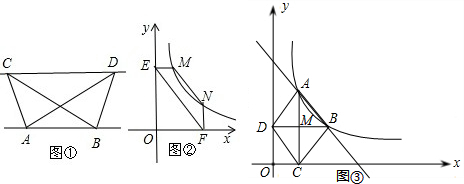
��1�������龳����ͼ�٣���֪��ABC���ABD�������ȣ����ж�AB��CD��λ�ù�ϵ����˵�����ɣ�
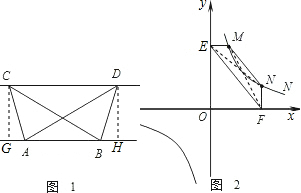
��2��̽�����֣���ͼ�ڣ���M��N�ڷ���������y=
��k��0����ͼ���ϣ�����M��ME��y�ᣬ����N��NF��x�ᣬ����ֱ�ΪE��F���㷢��MN��EF֮������������λ�ù�ϵ��˵��������ɣ�
��3��Ӧ�÷��֣���ͼ�ۣ���ƽ��ֱ������ϵ�У�����y=
��x��0��m�Dz�Ϊ0�ij�������ͼ����A��1��4����B��a��b��������a��1������A��x��Ĵ��ߣ�����ΪC������B��y��Ĵ��ߣ�����ΪD��AC��BD�ཻ�ڵ�M������AD��DC��CB��AB����֪AD=BC����ֱ��AB�ĺ�����ϵʽ��

��2��̽�����֣���ͼ�ڣ���M��N�ڷ���������y=
| k |
| x |
��3��Ӧ�÷��֣���ͼ�ۣ���ƽ��ֱ������ϵ�У�����y=
| m |
| x |
���㣺�����������ۺ���
ר�⣺
��������1���ֱ����C��D����CG��AB��DH��AB������ΪG��H������CG��DH���õ���ABC���ABDͬ�ף������������ε������ȣ����CG=DH������֤���ı���CGHDΪƽ���ı��Σ���AB��CD��
��2���ж�MN��EF�Ƿ�ƽ�У����ݣ�1���еĽ���ת��Ϊ֤��S��EFM=S��EFN���ɣ�
��3����֤�ı���ABCD�����Σ��ݴ˼������B�����꣬Ȼ�����ô���ϵ����������⣮
��2���ж�MN��EF�Ƿ�ƽ�У����ݣ�1���еĽ���ת��Ϊ֤��S��EFM=S��EFN���ɣ�
��3����֤�ı���ABCD�����Σ��ݴ˼������B�����꣬Ȼ�����ô���ϵ����������⣮
��� �⣺��1���ֱ����C��D����CG��AB��DH��AB������ΪG��H�����CGA=��DHB=90�㣬
�⣺��1���ֱ����C��D����CG��AB��DH��AB������ΪG��H�����CGA=��DHB=90�㣬
��CG��DH
�ߡ�ABC���ABD��������
��CG=DH��
���ı���CGHDΪƽ���ı���
��AB��CD��
��2����֤��������MF��NE��
���M��������x1��y1������N��������x2��y2����
�ߵ�M��N�ڷ���������y=
��k��0����ͼ���ϣ�
��x1y1=k��x2y2=k��
��ME��y�ᣬNF��x�ᣬ
��OE=y1��OF=x2��
��S��EFM=
x1•y1=
k��
S��EFN=
x2•y2=
k��
��S��EFM=S��EFN��
���ɣ�1���еĽ��ۿ�֪��MN��EF��
��3�����ݣ�2�����Եõ�AB��CD��
�֡�AD=BC��
���ı���ABCD��ƽ���ı��Σ�
�֡�AC��DB��
���ı���ABCD�����Σ�
��A�������ǣ�1��4����
��M�������ǣ�2��1������B�������ǣ�2��2����
��ֱ��AB�Ľ���ʽ��y=kx+b��
��������ã�
��
��ã�
��
��ֱ��AB�Ľ���ʽ�ǣ�y=-2x+6��
 �⣺��1���ֱ����C��D����CG��AB��DH��AB������ΪG��H�����CGA=��DHB=90�㣬
�⣺��1���ֱ����C��D����CG��AB��DH��AB������ΪG��H�����CGA=��DHB=90�㣬��CG��DH
�ߡ�ABC���ABD��������
��CG=DH��
���ı���CGHDΪƽ���ı���
��AB��CD��
��2����֤��������MF��NE��
���M��������x1��y1������N��������x2��y2����
�ߵ�M��N�ڷ���������y=
| k |
| x |
��x1y1=k��x2y2=k��
��ME��y�ᣬNF��x�ᣬ
��OE=y1��OF=x2��
��S��EFM=
| 1 |
| 2 |
| 1 |
| 2 |
S��EFN=
| 1 |
| 2 |
| 1 |
| 2 |
��S��EFM=S��EFN��
���ɣ�1���еĽ��ۿ�֪��MN��EF��
��3�����ݣ�2�����Եõ�AB��CD��
�֡�AD=BC��
���ı���ABCD��ƽ���ı��Σ�
�֡�AC��DB��
���ı���ABCD�����Σ�
��A�������ǣ�1��4����
��M�������ǣ�2��1������B�������ǣ�2��2����
��ֱ��AB�Ľ���ʽ��y=kx+b��
��������ã�
|
��ã�
|
��ֱ��AB�Ľ���ʽ�ǣ�y=-2x+6��
���������⿼���˷����������뼸�����ʵ��ۺ�Ӧ�ã�����һ���Ķ���������⣬��ȷ�����1���е�֤���ǽ������Ĺؼ���

��ϰ��ϵ�д�
 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�����Ŀ
���кϲ�ͬ������ȷ���ǣ�������
| A��2x2+3x4=5x6 |
| B��5xy2-3xy2=2 |
| C��7m2n-7mn2 |
| D��4ab2-5ab2=-ab2 |
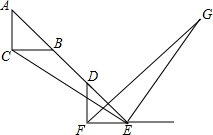 ��ͼ����ABC��һ������ֱ�������Σ���ACB=90�㣬����ABC��AB����ƽ�Ƶ���DEF������CE������E��EG��CE����DFE��ƽ�����ڵ�G����̽���߶�CE��EG��������ϵ����˵�����ɣ�
��ͼ����ABC��һ������ֱ�������Σ���ACB=90�㣬����ABC��AB����ƽ�Ƶ���DEF������CE������E��EG��CE����DFE��ƽ�����ڵ�G����̽���߶�CE��EG��������ϵ����˵�����ɣ�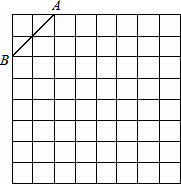 ��ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ�������
��ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ������� ��ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2��������M��·��O��A��C�˶���
��ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2��������M��·��O��A��C�˶���