题目内容
地震后重建1所A类学校比重建1所B类学校所需的资金少40万元,且重建1所A类学校和3所B类学校的校舍共需资金480万元.
(1)求重建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)某地区需重建A、B两类学校共8所,国家财政拨付的资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到A、B两类学校的资金分别为每所20万元和30万元,求有哪几种具体的改造方案?
(1)求重建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)某地区需重建A、B两类学校共8所,国家财政拨付的资金不超过770万元,地方财政投入的资金不少于210万元,其中地方财政投入到A、B两类学校的资金分别为每所20万元和30万元,求有哪几种具体的改造方案?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)等量关系为:改造一所A类学校和三所B类学校的校舍共需资金480万元;改造三所A类学校和一所B类学校的校舍共需资金400万元;
(2)关系式为:地方财政投资A类学校的总钱数+地方财政投资B类学校的总钱数≥210;国家财政投资A类学校的总钱数+国家财政投资B类学校的总钱数≤770.
(2)关系式为:地方财政投资A类学校的总钱数+地方财政投资B类学校的总钱数≥210;国家财政投资A类学校的总钱数+国家财政投资B类学校的总钱数≤770.
解答:解:(1)设改造一所A类学校的校舍需资金x万元,改造一所B类学校的校舍所需资金y万元,
则
,
解得
.
答:改造一所A类学校的校舍需资金90万元,改造一所B类学校的校舍所需资金130万元.
(2)设A类学校应该有a所,则B类学校有(8-a)所.
则
,
解得由①的a≤3,由②得a≥1,
∴1≤a≤3,即a=1,2,3.
答:有3种改造方案.
方案一:A类学校有1所,B类学校有7所;
方案二:A类学校有2所,B类学校有6所;
方案三:A类学校有3所,B类学校有5所.
则
|
解得
|
答:改造一所A类学校的校舍需资金90万元,改造一所B类学校的校舍所需资金130万元.
(2)设A类学校应该有a所,则B类学校有(8-a)所.
则
|
解得由①的a≤3,由②得a≥1,
∴1≤a≤3,即a=1,2,3.
答:有3种改造方案.
方案一:A类学校有1所,B类学校有7所;
方案二:A类学校有2所,B类学校有6所;
方案三:A类学校有3所,B类学校有5所.
点评:本题考查了二元一次方程组和不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.理解“国家财政拨付的改造资金不超过770万元,地方财政投入的资金不少于210万元”这句话中包含的不等关系是解决本题的关键.

练习册系列答案
相关题目
 如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.
如图,已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象相交于点A(-1,0)、B(2,-3),且二次函数与y轴相交于点C.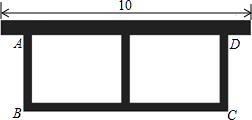 如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
 如图,抛物线
如图,抛物线 如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.
如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.