题目内容
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=| 3 |
| 4 |
(1)求点A,C的坐标;
(2)若反比例函数y=
| k |
| x |
(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题,勾股定理,相似三角形的应用
专题:压轴题
分析:(1)先求出一元二次方程x2-18x+72=0的两根就可以求出OA,OC的值,进而求出点A,C的坐标;
(2)先由勾股定理求出AB的值,得出AE的值,如图1,作EM⊥x轴于点M,由相似三角形的性质就可以求出EM的值,AM的值,就可以求出E的坐标,由待定系数法就可以求出结论;
(3)如图2,分别过C、E作CE的垂线交坐标轴三个点P1、P3、P4,可作出三个Q点,过E点作x轴的垂线与x轴交与p2,即可作出Q2,以CE为直径作圆交于y轴两个点P5、P6,使PC⊥PE,即可作出Q5、Q6.
(2)先由勾股定理求出AB的值,得出AE的值,如图1,作EM⊥x轴于点M,由相似三角形的性质就可以求出EM的值,AM的值,就可以求出E的坐标,由待定系数法就可以求出结论;
(3)如图2,分别过C、E作CE的垂线交坐标轴三个点P1、P3、P4,可作出三个Q点,过E点作x轴的垂线与x轴交与p2,即可作出Q2,以CE为直径作圆交于y轴两个点P5、P6,使PC⊥PE,即可作出Q5、Q6.
解答:解:(1)∵x2-18x+72=0
∴x1=6,x2=12.
∵OA>OC,
∴OA=12,OC=6.
∴A(12,0),C(-6,0);
(2)∵tan∠ABO=
,
∴
=
,
∴
=
,
∴OB=16.
在Rt△AOB中,由勾股定理,得
AB=
=20.
∵BE=5,
∴AE=15.
如图1,作EM⊥x轴于点M,
∴EM∥OB.
∴△AEM∽△ABO,
∴
=
=
,
∴
=
=
,
∴EM=12,AM=9,
∴OM=12-9=3,
∴E(3,12),
∴12=
,
∴k=36;
(3)满足条件的点Q的个数是6,如图2所示,
x轴的下方的Q4(10,-12),Q6(-3,6-3
);

如图①,∵E(3,12),C(-6,0),
∴CG=9,EG=12,
∴EG2=CG•GP,
∴GP=16,
∵△CPE与△PCQ中心对称,
∴CH=GP=16,QH=EG=12,
∵OC=6,
∴OH=10,
∴Q(10,-12),

如图②∵E(3,12),C(-6,0),
∴CG=9,EG=12,
∴CE=15,
∵MN=
CG=
,
∴MK=
-3=
,
∴PK=
=3
,
∴PH=3
-
=3
-6,
根据轴对称和中心对称的性质,
∴Q(-3,6-3
),
∴x1=6,x2=12.
∵OA>OC,
∴OA=12,OC=6.
∴A(12,0),C(-6,0);
(2)∵tan∠ABO=
| 3 |
| 4 |
∴
| OA |
| OB |
| 3 |
| 4 |
∴
| 12 |
| OB |
| 3 |
| 4 |
∴OB=16.

在Rt△AOB中,由勾股定理,得
AB=
| 162+122 |
∵BE=5,
∴AE=15.
如图1,作EM⊥x轴于点M,
∴EM∥OB.
∴△AEM∽△ABO,
∴
| EM |
| BO |
| AM |
| AO |
| AE |
| AB |
∴
| EM |
| 16 |
| AM |
| 12 |
| 15 |
| 20 |
∴EM=12,AM=9,
∴OM=12-9=3,
∴E(3,12),
∴12=
| k |
| 3 |
∴k=36;
(3)满足条件的点Q的个数是6,如图2所示,

x轴的下方的Q4(10,-12),Q6(-3,6-3
| 6 |

如图①,∵E(3,12),C(-6,0),
∴CG=9,EG=12,
∴EG2=CG•GP,
∴GP=16,
∵△CPE与△PCQ中心对称,
∴CH=GP=16,QH=EG=12,
∵OC=6,
∴OH=10,
∴Q(10,-12),

如图②∵E(3,12),C(-6,0),
∴CG=9,EG=12,
∴CE=15,
∵MN=
| 1 |
| 2 |
| 9 |
| 2 |
∴MK=
| 9 |
| 2 |
| 3 |
| 2 |
∴PK=
(
|
| 6 |
∴PH=3
| 6 |
| EG |
| 2 |
| 6 |
根据轴对称和中心对称的性质,
∴Q(-3,6-3
| 6 |
点评:本题考查了一次函数的交点坐标的求法以及勾股定理的运用,三角函数的应用,三角形相似对应边成比例等.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
已知正六边形的面积为6
,则其边长为( )
| 3 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、2
|
 以点A(0,4),B(8,4),C(0,8)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.
以点A(0,4),B(8,4),C(0,8)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.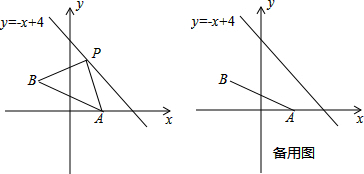
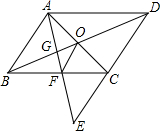 点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
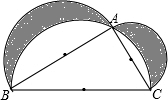 如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积. 如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长.
如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长.