题目内容
如图,已知点A(2,0)、B(-1,1),点P是直线y=-x+4上任意一点.
(1)当点P在什么位置时,△PAB的周长最小?求出点P的坐标及周长的最小值;
(2)在(1)的条件下,求出△PAB的面积.
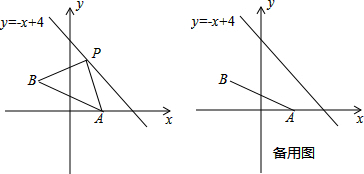
(1)当点P在什么位置时,△PAB的周长最小?求出点P的坐标及周长的最小值;
(2)在(1)的条件下,求出△PAB的面积.
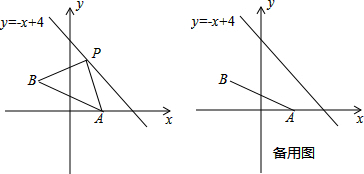
考点:轴对称-最短路线问题,一次函数图象上点的坐标特征
专题:
分析:(1)先根据对称找出P点的位置,求出A的对称点C的坐标,求出直线BC解析式,求出两函数组成的方程组的解,即可求出P的坐标,即可求出答案;
(2)根据S△PAB=S△PAF-S△BAF代入求出即可.
(2)根据S△PAB=S△PAF-S△BAF代入求出即可.
解答:解:(1)作出点A关于直线y=-x+4的对称点C,连结BC交直线于点P,
∴PA=PC,AD=CD,
则PB+PA=PB+PC=BC,
由直线y=-x+4得与x轴上的交点D为(4,0)、与y轴的交点为E为(0,4),
∴OD=OE=4,则∠ODE=45°,则∠ADC=90°,
∴AD=CD=2,
∴点C的坐标是(4,2),
设直线BC的解析式为y=kx+b,则有
,
解得:k=
,b=
,
即直线BC的解析式为:y=
x+
.
由方程组
得:
,
即P的坐标是(
,
),
由勾股定理得BC=
、AB=
,
∴△PAB的周长是
+
;
(2)直线y=x+4与x轴交于F点,如图2,
由直线BC的解析式y=
x+
得:点F的坐标是(-6,0),
∴S△PAB=S△PAF-S△BAF=
×AF×(
-1)=
.
∴PA=PC,AD=CD,
则PB+PA=PB+PC=BC,
由直线y=-x+4得与x轴上的交点D为(4,0)、与y轴的交点为E为(0,4),
∴OD=OE=4,则∠ODE=45°,则∠ADC=90°,
∴AD=CD=2,
∴点C的坐标是(4,2),
设直线BC的解析式为y=kx+b,则有
|
解得:k=
| 1 |
| 5 |
| 6 |
| 5 |
即直线BC的解析式为:y=
| 1 |
| 5 |
| 6 |
| 5 |
由方程组
|
|
即P的坐标是(
| 7 |
| 3 |
| 5 |
| 3 |
由勾股定理得BC=
| 26 |
| 10 |
∴△PAB的周长是
| 26 |
| 10 |

(2)直线y=x+4与x轴交于F点,如图2,
由直线BC的解析式y=
| 1 |
| 5 |
| 6 |
| 5 |
∴S△PAB=S△PAF-S△BAF=
| 1 |
| 2 |
| 5 |
| 3 |
| 8 |
| 3 |
点评:本题考查了轴对称性质,勾股定理,用待定系数法求一次函数的解析式,三角形的面积等知识点的应用,题目比较典型,但是有一定的难度.

练习册系列答案
相关题目
为了解某校初三年级500名学生800米跑的成绩,从中抽取了100名学生的800米跑成绩进行统计.下列说法错误的是( )
| A、这种调查方式是抽样调查 |
| B、每名学生的800米跑成绩是个体 |
| C、100名学生是总体的一个样本 |
| D、100是样本容量 |
 如图,在矩形ABCD中,E,F分别是边AD,BC上的点,ED=BF,连接EF,EC,EF与对角线BD交于点O,且CE=CF
如图,在矩形ABCD中,E,F分别是边AD,BC上的点,ED=BF,连接EF,EC,EF与对角线BD交于点O,且CE=CF 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=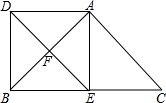 如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.