题目内容
11.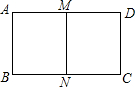 如图,在矩形ABCD中,AD>AB,将其沿AD、BC的中点M,N对折后,得到的两个矩形与原矩形相似,求$\frac{AD}{AB}$的值.
如图,在矩形ABCD中,AD>AB,将其沿AD、BC的中点M,N对折后,得到的两个矩形与原矩形相似,求$\frac{AD}{AB}$的值.
分析 根据相似多边形的性质得到$\frac{AB}{AD}$=$\frac{AM}{AB}$,根据中点的性质计算即可.
解答 解:∵矩形ABNM∽矩形BCDA,
∴$\frac{AB}{AD}$=$\frac{AM}{AB}$,即$\frac{AB}{AD}$=$\frac{\frac{1}{2}AD}{AB}$,
∴$\frac{A{D}^{2}}{A{B}^{2}}$=2,
∴$\frac{AD}{AB}$=$\sqrt{2}$.
点评 本题考查的是相似多边形的性质,相似多边形的性质为:对应角相等;对应边的比相等.

练习册系列答案
相关题目
1.如图,用12块相同的小长方形瓷砖拼成一个大的长方形,则每个小长方形瓷砖的面积是( )


| A. | 175cm2 | B. | 300cm2 | C. | 375cm2 | D. | 336cm2 |
3.下列说法正确的是( )
| A. | 直线CD和直线DC表示两条不同的直线 | |
| B. | 射线CD和射线DC表示两条不同的射线 | |
| C. | 线段CD和线段DC表示两条不同的线段 | |
| D. | 直线CD和直线a不能表示同一条直线 |
20.与$\sqrt{5}$是同类二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{50}$ | C. | $\sqrt{20}$ | D. | $\sqrt{18}$ |
 己知:线段AB=r.求作:半径为r的圆内接正三角形、正四边形和正六边形.
己知:线段AB=r.求作:半径为r的圆内接正三角形、正四边形和正六边形.
 如图,下列语句:
如图,下列语句: