题目内容
2.已知圆柱的底面积为9πcm2,则底面周长为6πcm;若侧面积为18πcm2,则圆锥的母线长为6cm.分析 设圆柱的底面圆的半径为r,根据圆的面积公式可求出r=3,再利用圆的周长公式计算圆柱的底面圆的周长;设圆锥的母线长为l,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到$\frac{1}{2}$•6π•l=18π,然后解方程求出l即可.
解答 解:设圆柱的底面圆的半径为r,则
πr2=9π,
解得r=3.
则圆柱的底面圆的周长为6πcm;
设圆锥的母线长为l,则
$\frac{1}{2}$•6π•l=18π,
解得l=6.
故答案为6πcm,6cm.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了圆柱的计算.

练习册系列答案
相关题目
12.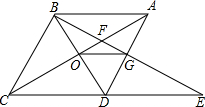 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:
如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:
①OG=$\frac{1}{2}$AB;
②与△EGD全等的三角形共有5个;
③S四边形ODGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
其中正确的是( )
 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:
如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①OG=$\frac{1}{2}$AB;
②与△EGD全等的三角形共有5个;
③S四边形ODGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
其中正确的是( )
| A. | ①④ | B. | ①③④ | C. | ①②③ | D. | ②③④ |
7.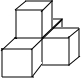 如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
 如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )| A. | 从正面看到的形状图面积最小 | B. | 从左面看到的形状图面积最小 | ||
| C. | 从上面看到的形状图面积最小 | D. | 三个方向看到的形状图面积一样大 |
12.下列物体的形状属于球体的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图:
如图: 如图,AB是⊙O的直径,D为$\widehat{AC}$的中点,∠ABC=40°,则∠C=110°.
如图,AB是⊙O的直径,D为$\widehat{AC}$的中点,∠ABC=40°,则∠C=110°. 如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.
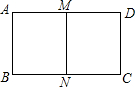 如图,在矩形ABCD中,AD>AB,将其沿AD、BC的中点M,N对折后,得到的两个矩形与原矩形相似,求$\frac{AD}{AB}$的值.
如图,在矩形ABCD中,AD>AB,将其沿AD、BC的中点M,N对折后,得到的两个矩形与原矩形相似,求$\frac{AD}{AB}$的值.