题目内容
2.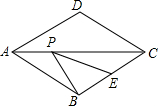 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | 5 |
分析 连接BD,DE,则DE的长即为PE+PB的最小值,再根据菱形ABCD中,∠ABC=120°得出∠BCD的度数,进而判断出△BCD是等边三角形,故△CDE是直角三角形,根据勾股定理即可得出DE的长.
解答 解:连接BD,DE,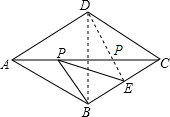
∵四边形ABCD是菱形,
∴B、D关于直线AC对称,
∴DE的长即为PE+PB的最小值,
∵∠ABC=120°,
∴∠BCD=60°,
∴△BCD是等边三角形,
∵E是BC的中点,
∴DE⊥BC,CE=$\frac{1}{2}$BC=$\frac{1}{2}$×2=1,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
故选:A
点评 本题考查的是轴对称-最短路线问题,熟知菱形的性质及两点直线线段最短是解答此题的关键.

练习册系列答案
相关题目
13.下列各数是4的平方根的是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |
14.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{24}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{{x}^{2}+{y}^{2}}$ |
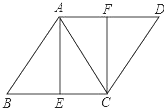 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.


