题目内容
17.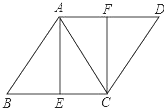 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.
分析 (1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;
(2)利用勾股定理得出AE的长,进而求出菱形的面积.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=$\frac{1}{2}$AD,EC=$\frac{1}{2}$BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠AEC=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)解:在Rt△ABE中,AE=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
所以,S菱形ABCD=6×3$\sqrt{3}$=18$\sqrt{3}$.
点评 此题主要考查了矩形的判定以及菱形的性质与面积求法,正确掌握矩形的判定方法是解题关键.

练习册系列答案
相关题目
7.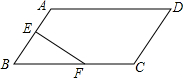 如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
 如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )
如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为( )| A. | 1:4 | B. | 1:8 | C. | 1:5 | D. | 1:7 |
5.使分式$\frac{x-2012}{2x-8}$有意义的x的取值范围是( )
| A. | x=4 | B. | x≠4 | C. | x=-4 | D. | x≠-4 |
2.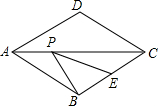 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | 5 |
 作三角形关于点成中心对称的图形:已知△ABC和点O,画出△DEF,使△DEF与△ABC关于O成中心对称.
作三角形关于点成中心对称的图形:已知△ABC和点O,画出△DEF,使△DEF与△ABC关于O成中心对称.