题目内容
13.下列各数是4的平方根的是( )| A. | ±2 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |
分析 一个正数的平方根有两个,它们互为相反数,据此求出4的平方根是多少即可.
解答 解:∵±$\sqrt{4}$=±2,
∴是4的平方根的是±2.
故选:A.
点评 此题主要考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元.
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元.
5.使分式$\frac{x-2012}{2x-8}$有意义的x的取值范围是( )
| A. | x=4 | B. | x≠4 | C. | x=-4 | D. | x≠-4 |
2.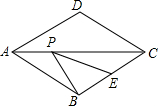 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | 5 |
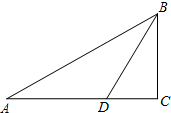 如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.