题目内容
10.计算:(1)(-$\sqrt{3}$)2+|-2|-(-2)0;
(2)解不等式组$\left\{\begin{array}{l}4(x+1)≤7x+10\\ x-5<\frac{x-8}{3}\end{array}\right.$,并写出它的所有非负整数解.
分析 (1)原式利用乘方的意义,绝对值的代数意义,以及零指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的方法部分确定出不等式组的解集,即可确定出所有非负整数解.
解答 解:(1)原式=3+2-1=4;
(2)$\left\{\begin{array}{l}{4(x+1)≤7x+10①}\\{x-5<\frac{x-8}{3}②}\end{array}\right.$,
由①得:x≥-2,
由②得:x<3.5,
则不等式组的解集为-2<x≤3.5,
则所有非负整数解为0,1,2,3.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
20.根据下列表格中关于x的代数式ax2+bx+c的值与x的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解的范围是( )
| x | 5.12 | 5.13 | 5.14 | 5.15 |
| ax2+bx+c | -0.04 | -0.02 | 0.01 | 0.03 |
| A. | 5.14<x<5.15 | B. | 5.13<x<5.14 | C. | 5.12<x<5.13 | D. | 5.10<x<5.12 |
5.使分式$\frac{x-2012}{2x-8}$有意义的x的取值范围是( )
| A. | x=4 | B. | x≠4 | C. | x=-4 | D. | x≠-4 |
2.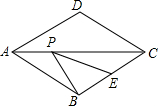 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
 如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AD=2,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | 5 |
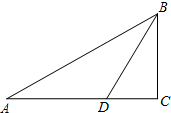 如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.