题目内容
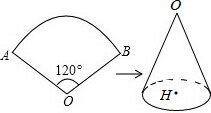 已知如图,扇形AOB的圆心角为120°,半径OA为6cm.
已知如图,扇形AOB的圆心角为120°,半径OA为6cm.(1)求扇形AOB的弧长和扇形面积;
(2)若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.
考点:圆锥的计算,弧长的计算,扇形面积的计算
专题:计算题
分析:(1)根据扇形的弧长公式和扇形的面积公式求解;
(2)设圆锥底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到2πr=4π,解得r=2,然后根据勾股定理计算OH.
(2)设圆锥底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到2πr=4π,解得r=2,然后根据勾股定理计算OH.
解答: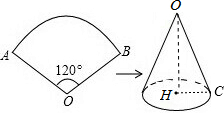 解:(1)扇形AOB的弧长=
解:(1)扇形AOB的弧长=
=4π(cm);
扇形AOB的扇形面积=
=12π(cm2);
(2)如图,设圆锥底面圆的半径为r,
所以2πr=4π,解得r=2,
在Rt△OHC中,HC=2,OC=6,
所以OH=
=4
(cm).
 解:(1)扇形AOB的弧长=
解:(1)扇形AOB的弧长=| 120•π•6 |
| 180 |
扇形AOB的扇形面积=
| 120•π•62 |
| 360 |
(2)如图,设圆锥底面圆的半径为r,
所以2πr=4π,解得r=2,
在Rt△OHC中,HC=2,OC=6,
所以OH=
| OC2-HC2 |
| 2 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线.也考查了扇形的弧长和面积公式.

练习册系列答案
相关题目
已知菱形的周长为40cm,一条对角线长为16cm,则这个菱形的面积为( )cm2.
| A、108 | B、114 |
| C、64 | D、96 |
 如图,双曲线y=
如图,双曲线y= 如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,已知DE=3,EF=4,FB=3,则BC=
如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,已知DE=3,EF=4,FB=3,则BC=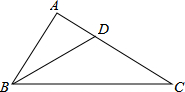 已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.
已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.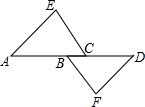 如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.
如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.