题目内容
 如图,双曲线y=
如图,双曲线y=| k |
| x |
| 5 |
(1)求双曲线的解析式;
(2)求点E,B,F的坐标;
(3)若点P为x轴上一动点,求出点P的坐标,使得△POE为等腰三角形.
考点:反比例函数综合题
专题:综合题
分析:(1)设矩形AOCB长为a,宽为b,表示出AF,OA,CE,OC,进而表示出三角形AOF与三角形COE面积,得到四边形BEOF面积,根据三角形AOF面积与四边形BEOF面积之比求出三角形AOF面积,利用反比例函数k的几何意义求出k的值,即可确定出解析式;
(2)由k的值,利用反比例函数k的几何意义求出三角形AOF面积,得出ab=4,再利用勾股定理列出关于a与b的方程,的求出方程的解得到a与b的值,即可确定出各点的坐标;
(3)分三种情况考虑:以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形;以E为圆心,OE长为半径画弧,与x轴交于一点P;做出线段OE的垂直平分线,交x轴于点P,分别求出P坐标即可.
(2)由k的值,利用反比例函数k的几何意义求出三角形AOF面积,得出ab=4,再利用勾股定理列出关于a与b的方程,的求出方程的解得到a与b的值,即可确定出各点的坐标;
(3)分三种情况考虑:以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形;以E为圆心,OE长为半径画弧,与x轴交于一点P;做出线段OE的垂直平分线,交x轴于点P,分别求出P坐标即可.
解答: 解:(1)矩形AOCB长为a,宽为b,
解:(1)矩形AOCB长为a,宽为b,
则有AF=
b,OA=a,CE=
a,OC=b,
∴S△AOF=
AF•OA=
ab,S△COE=
CE•OC=
ab,
∴S四边形BEOF=ab-
ab-
ab=
ab,
∴
=
=
,
∵S四边形BEOF=2,
∴S△AOF=1,即
|k|=1,
∵反比例函数图象位于第一象限,
∴k=2,
则反比例解析式为y=
;
(2)由k=2,得到S△AOF=
AF•OA=
ab=1,即ab=4①,
在Rt△COE中,根据勾股定理得:OC2+CE2=OE2,即b2+
a2=5②,
联立①②解得:a=b=2或a=4,b=1,
当a=b=2时,E(1,2),F(2,1),B(2,2);
当a=4,b=1时,E(2,1),F(4,
),B(4,1);
(3)当a=b=2时,
以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形,P坐标为(
,0);(-
,0);
以E为圆心,OE长为半径画弧,与x轴交于一点,此时EP=EO=
,P坐标为(2,0);
做出线段OE的垂直平分线,交x轴于点P,此时P(2.5,0);
当a=4,b=1时,
以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形,P坐标为(
,0);(-
,0);
以E为圆心,OE长为半径画弧,与x轴交于一点,此时EP=EO=
,P坐标为(4,0);
做出线段OE的垂直平分线,交x轴于点P,此时P(
,0).
 解:(1)矩形AOCB长为a,宽为b,
解:(1)矩形AOCB长为a,宽为b,则有AF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOF=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴S四边形BEOF=ab-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| S△AOF |
| S四边形BEOF |
| ||
|
| 1 |
| 2 |
∵S四边形BEOF=2,
∴S△AOF=1,即
| 1 |
| 2 |
∵反比例函数图象位于第一象限,
∴k=2,
则反比例解析式为y=
| 2 |
| x |
(2)由k=2,得到S△AOF=
| 1 |
| 2 |
| 1 |
| 4 |
在Rt△COE中,根据勾股定理得:OC2+CE2=OE2,即b2+
| 1 |
| 4 |
联立①②解得:a=b=2或a=4,b=1,
当a=b=2时,E(1,2),F(2,1),B(2,2);
当a=4,b=1时,E(2,1),F(4,
| 1 |
| 2 |
(3)当a=b=2时,
以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形,P坐标为(
| 5 |
| 5 |
以E为圆心,OE长为半径画弧,与x轴交于一点,此时EP=EO=
| 5 |
做出线段OE的垂直平分线,交x轴于点P,此时P(2.5,0);
当a=4,b=1时,
以O为圆心,OE长为半径画弧,与x轴交于两点,此时△POE为等腰三角形,P坐标为(
| 5 |
| 5 |
以E为圆心,OE长为半径画弧,与x轴交于一点,此时EP=EO=
| 5 |
做出线段OE的垂直平分线,交x轴于点P,此时P(
| 9 |
| 4 |
点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,反比例函数k的几何意义,等腰三角形的性质,熟练掌握反比例函数k的几何意义是解本题的关键.

练习册系列答案
相关题目
一架250cm的梯子斜靠在墙上,这时梯足与墙的终端距离为70cm,如果梯子顶端沿墙下滑40cm,那么梯足将向外滑动( )
| A、150cm | B、90cm |
| C、80cm | D、40cm |

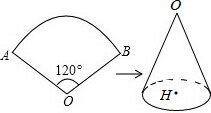 已知如图,扇形AOB的圆心角为120°,半径OA为6cm.
已知如图,扇形AOB的圆心角为120°,半径OA为6cm. 如图,点E、F分别是菱形ABCD的边BC、CD上的一点,且∠EAF=∠ADC=60°,求证:△BAE≌△CAF.
如图,点E、F分别是菱形ABCD的边BC、CD上的一点,且∠EAF=∠ADC=60°,求证:△BAE≌△CAF.