题目内容
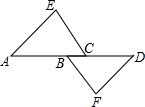 如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.
如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.(1)求AC的长;
(2)求证:CE∥BF.
考点:全等三角形的性质
专题:
分析:(1)根据全等三角形对应边相等可得AC=BD,然后根据AC=
(AD+BC)代入数据计算即可得解;
(2)根据全等三角形对应角相等可得∠ACE=∠DBF,再根据内错角相等,两直线平行证明即可.
| 1 |
| 2 |
(2)根据全等三角形对应角相等可得∠ACE=∠DBF,再根据内错角相等,两直线平行证明即可.
解答:(1)解:∵△ACE≌△DBF,
∴AC=BD,
∴AC=
(AD+BC)=
×(8+2)=5;
(2)证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE∥BF.
∴AC=BD,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:∵△ACE≌△DBF,
∴∠ACE=∠DBF,
∴CE∥BF.
点评:本题考查了全等三角形的性质,平行线的判定,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
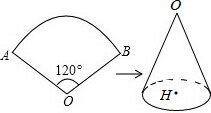 已知如图,扇形AOB的圆心角为120°,半径OA为6cm.
已知如图,扇形AOB的圆心角为120°,半径OA为6cm. 如图,点E、F分别是菱形ABCD的边BC、CD上的一点,且∠EAF=∠ADC=60°,求证:△BAE≌△CAF.
如图,点E、F分别是菱形ABCD的边BC、CD上的一点,且∠EAF=∠ADC=60°,求证:△BAE≌△CAF.