题目内容
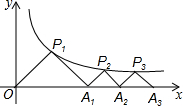 如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=| 9 |
| x |
考点:反比例函数图象上点的坐标特征,等腰直角三角形
专题:计算题
分析:作P1B⊥x1轴于B,P2C⊥x轴于C,P3D⊥x轴于D,如图,根据等腰直角三角形的性质得x1=y1,根据反比例函数图象上点的坐标特征得到x1•y1=9,易得y1=3,则A1(6,0),于是有x2=6+y2,再利用x2•y2=9解得y2=3
-3,同理得到x3=6
+y3,yn=3
-3
,所以y1+y2+…+yn=3
.
| 2 |
| 2 |
| n |
| n-1 |
| n |
解答:解: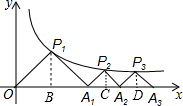 作P1B⊥x1轴于B,P2C⊥x轴于C,P3D⊥x轴于D,如图,
作P1B⊥x1轴于B,P2C⊥x轴于C,P3D⊥x轴于D,如图,
∵△OP1A1为等腰直角三角形,
∴x1=y1,
而x1•y1=9,
∴y1=3,
∴A1(6,0),
∴x2=6+y2,
∵x2•y2=9,
∴(6+y2)•y2=9,解得y2=3
-3,
∴y1+y2=3
;
∴A1A2=6
-6,
∴OA2=6
,
∴x3=6
+y3,
而x3•y3=9,
∴(6
+y3)•y3=9,解得y3=3
-3
,
∴yn=3
-3
,
∴y1+y2+…+yn=3++3
-3+3
-3
+3
-3
=3
.
故答案为3
,3
.
 作P1B⊥x1轴于B,P2C⊥x轴于C,P3D⊥x轴于D,如图,
作P1B⊥x1轴于B,P2C⊥x轴于C,P3D⊥x轴于D,如图,∵△OP1A1为等腰直角三角形,
∴x1=y1,
而x1•y1=9,
∴y1=3,
∴A1(6,0),
∴x2=6+y2,
∵x2•y2=9,
∴(6+y2)•y2=9,解得y2=3
| 2 |
∴y1+y2=3
| 2 |
∴A1A2=6
| 2 |
∴OA2=6
| 2 |
∴x3=6
| 2 |
而x3•y3=9,
∴(6
| 2 |
| 3 |
| 2 |
∴yn=3
| n |
| n-1 |
∴y1+y2+…+yn=3++3
| 2 |
| 3 |
| 2 |
| n |
| n-1 |
| n |
故答案为3
| 2 |
| n |
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了等腰直角三角形的性质.
| k |
| x |

练习册系列答案
相关题目
 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则BE的长是( )| A、1 | B、2 | C、4 | D、6 |
下列长度的三条线段,能组成三角形的是( )
| A、3,4,8 |
| B、5,6,11 |
| C、3,3,7 |
| D、2,2,2 |
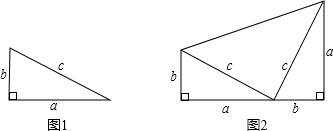
 已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD.
已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD.