题目内容
1.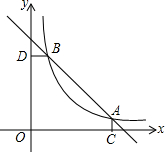 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点. (1)求函数y2的表达式;
(2)过A作AC⊥x轴,过B作BD⊥y轴,试问在线段AB上是否存在点P,使S△PBD=2S△PAC?若存在请求出P点坐标;若不存在请说明理由.
分析 (1)把A、B两点坐标代入直线AB解析式可求得A、B两点的坐标,再把B点坐标代入反比例函数解析式可求得k,可求得函数y2的表达式;
(2)设出P点坐标为(x,-x+4),根据三角形的面积关系可得到关于x的方程,可求得P点坐标.
解答 解:
(1)∵函数y1的图象过A、B两点,
∴把A、B两点分别代入函数y1的解析式可得$\left\{\begin{array}{l}{2b-9=-3a+4}\\{b-2=-a+4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=5}\end{array}\right.$,
∴A(3,1),B(1,3),
∵函数y2的图象过A点,
∴1=$\frac{k}{3}$,解得k=3,
∴y2=$\frac{3}{x}$;
(2)由(1)知A(3,1),B(1,3),
∴BD=AC=1,
∵P点在线段AB上,
∴设P点坐标为(x,-x+4),其中1≤x≤3,
则P到AC的距离为hA=3-x,P到BD的距离为hB=3-(-x+4)=x-1,
∴S△PBD=$\frac{1}{2}$BD•hB=$\frac{1}{2}$×1×(x-1)=$\frac{1}{2}$(x-1),S△PAC=$\frac{1}{2}$AC•hA=$\frac{1}{2}$×1×(3-x)=$\frac{1}{2}$(3-x),
∵S△PBD=2S△PAC,
∴$\frac{1}{2}$(x-1)=3-x,解得x=$\frac{7}{3}$,且1≤$\frac{7}{3}$≤3,符合条件,此时-x+4=$\frac{5}{3}$,
∴P($\frac{7}{3}$,$\frac{5}{3}$),
综上可知存在满足条件的点P,其坐标为($\frac{7}{3}$,$\frac{5}{3}$).
点评 本题主要考查一次函数和反比例函数的交点问题,在(1)中掌握交点坐标满足两函数解析式是解题的关键,在(2)中用P点坐标分别表示出△PBD和△PAC的面积是解题的关键.

| A. | 0.8×107 | B. | 8×10-8 | C. | 8×10-7 | D. | 8×10-6 |
| A. |  | B. |  | C. |  | D. |  |
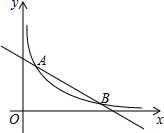 如图,平面直角坐标系中,A、B两点的纵坐标分别为8和2,直线AB与y轴所夹锐角为60°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A、B两点,则k=16$\sqrt{3}$.
如图,平面直角坐标系中,A、B两点的纵坐标分别为8和2,直线AB与y轴所夹锐角为60°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A、B两点,则k=16$\sqrt{3}$.