题目内容
10．
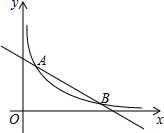如图，平面直角坐标系中，A、B两点的纵坐标分别为8和2，直线AB与y轴所夹锐角为60°，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过A、B两点，则k=16$\sqrt{3}$．
分析 分别过A、B作y轴的垂线，垂足分别为C、D，过A作AE⊥x轴，交BD于点F，由点A、B的纵坐标可表示出其横坐标，可用k表示出AF、BF的长，再利用AB与y轴的夹角为60°，可得到关于k的方程，可求得k的值．
解答 解：如图，分别过A、B作y轴的垂线，垂足分别为C、D，
过A作AE⊥x轴于点E，交BD于点F，
∵A、B两点在反比例函数图象上，且A、B两点的纵坐标分别为8和2，
∴A、B两点的横坐标分别为$\frac{k}{8}$和$\frac{k}{2}$，
∴AE=8，EF=2，DF=$\frac{k}{8}$，DB=$\frac{k}{2}$，
∴AF=AE-EF=6，BF=BD-DF=$\frac{3}{8}$k，
∵直线AB与y轴的夹角为60°，
∴∠BAF=60°，
∴$\frac{BF}{AF}$=tan60°=$\sqrt{3}$，
∴BF=$\sqrt{3}$AF，
∴$\frac{3}{8}$k=6$\sqrt{3}$，
解得k=16$\sqrt{3}$．
故答案为：16$\sqrt{3}$．
点评 本题主要考查一次函数和反比例函数的交点问题，根据条件构造三角形，找到AF和BF的关系是解题的关键，注意充分利用点的坐标与函数解析式的关系．
练习册系列答案
相关题目
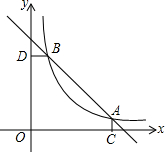如图，函数y1=-x+4的图象与函数y2=$\frac{k}{x}$（x＞0）的图象交于A（3a，2b-9）、B（a，b-2）两点． 
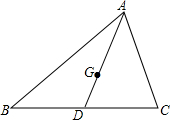如图，AD为△ABC的中线，G为△ABC的重心，若S△BGC=2，则S△ABD=3．
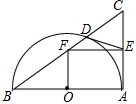如图，以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D，过D作半圆的切线与边AC交于点E，过E作EF∥AB，与BC交于点F．若AB=20，OF=7.5，则CD的长为（ ）
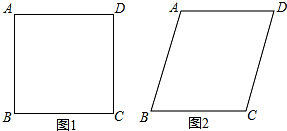将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B=90°时，如图1，测得AC=2，当∠B=60°时，如图2，AC=$\sqrt{2}$．