题目内容
6.有四张不透明卡片,分别写有实数$\sqrt{2}$,-1,$\sqrt{3}$,$\frac{1}{5}$,除正面的数不同外其余都相同,将它们背面朝上洗匀后,从中任取一张卡片,取到的数是无理数的可能性大小是$\frac{1}{2}$.分析 首先判断出实数$\sqrt{2}$,-1,$\sqrt{3}$,$\frac{1}{5}$中,无理数有几个;然后根据求可能性大小的方法,用无理数的个数除以4,求出取到的数是无理数的可能性大小是多少即可.
解答 解:∵实数$\sqrt{2}$,-1,$\sqrt{3}$,$\frac{1}{5}$中,$\sqrt{2}$,$\sqrt{3}$是无限不循环小数,
∴无理数有2个,
∴取到的数是无理数的可能性大小是:
2÷4=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 (1)此题主要考查了可能性的大小,要熟练掌握,解答此题的关键是求出无理数一共有多少个.
(2)此题还考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.

练习册系列答案
相关题目
14.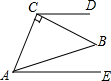 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
 如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )
如图,CD∥AE,∠ACB=90°,AC=BC,∠BCD=20°,则∠EAB的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.
如图,以点P为顶点,射线AB为一边,利用尺规作∠QPB,∠QPB=∠CAB.并说明PQ与AC的位置关系.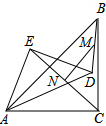 已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.
已知等腰Rt△ABC和等腰Rt△ABC中,∠ACB=∠AED=90°,且AD=AC,若点M、N分别是DB、EC的中点,证明:MN⊥EC,MN=$\frac{1}{2}$EC.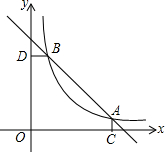 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点. 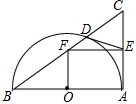 如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )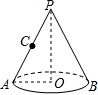 小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.
小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.