题目内容

11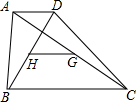．如图，在四边形ABCD中，AD∥BC，AB与CD不平行，H、G分别是两条对角线BD、AC的中点，求证：GH∥AD，且GH=$\frac{1}{2}$（BC-AD）．

分析 连接AH并延长交BC于E，根据相似三角形的性质得到AH=HE，BE=AD，根据三角形中位线定理得到HG∥EC，HG=$\frac{1}{2}$EC，证明结论．

解答 证明：连接AH并延长交BC于E，
∵AD∥BC，H是BD的中点，
∴AH=HE，BE=AD，
G是AC的中点，
∴HG∥EC，HG=$\frac{1}{2}$EC，
∴GH∥AD，GH=$\frac{1}{2}$（BC-BE）=$\frac{1}{2}$（BC-AD）．

点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．

练习册系列答案
相关题目
19．已知实数x，y满足$\sqrt{2x+y-5}$+x2+4y2=4xy，则（x-y）2017的值为（　　）
A．0B．-1C．1D．2016
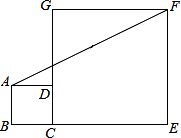2．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，C到直线AF的距离是$\frac{3\sqrt{5}}{5}$．
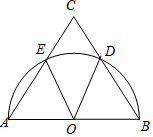19．如图，O为等腰三角形ABC的底边AB的中点，以AB为直径的半圆分别交AC，BC于于点E．
（1）求证：∠AOE=∠BOD．
（2）求证：$\widehat{AD}=\widehat{BE}$．
6．小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$，求△ABC的面积．
小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．

请回答：
（1）求图1中△ABC的面积；
参考小明解决问题的方法，完成下列问题：
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．
①利用构图法在答题卡的图2中画出三边长分别为$\sqrt{13}$、2$\sqrt{5}$、$\sqrt{29}$的格点△DEF；
②计算△DEF的面积是8．
（3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若PQ=2$\sqrt{2}$，PR=$\sqrt{13}$，QR=$\sqrt{17}$，求六边形AQRDEF的面积．
16．在△ABC中，AB=10，AC=10，BC=8，则△ABC是等腰三角形．
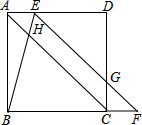3．如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连结EF与边CD相交于点G，连结BE与对角线AC相交于点H，AE=CF，BE=EG．
（1）求证：EF∥AC；   （2）求∠BEF大小．
20．在一次函数y=2x-2的图象上，到x轴的距离等于2的点的坐标是（0，-2）或（2，2）．
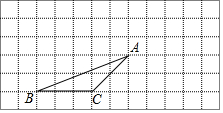1．画图并填空：如图，△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上，将△ABC向右平移3格，再向上平移2格．
（1）请在图中画出平移后的△A'B'C'；   
（2）△ABC的面积为3；
（3）若AB的长约为5.4，求出AB边上的高．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网