题目内容
19.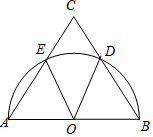 如图,O为等腰三角形ABC的底边AB的中点,以AB为直径的半圆分别交AC,BC于于点E.
如图,O为等腰三角形ABC的底边AB的中点,以AB为直径的半圆分别交AC,BC于于点E.(1)求证:∠AOE=∠BOD.
(2)求证:$\widehat{AD}=\widehat{BE}$.
分析 (1)根据等腰三角形的性质得出∠A=∠B,∠AOE=∠A,∠BOD=∠B,即可求出答案;
(2)求出∠AOD=∠BOE,即可得出答案.
解答 证明:(1)∵△ABC是等腰三角形,
∴∠A=∠B,
∵OE=OA,OD=OB,
∴∠AOE=∠A,∠BOD=∠B,
∴∠AOE=∠BOD;
(2)∵∠AOE=∠BOD,
∴∠AOD+∠DOE=∠BOD+∠DOE,
∴∠AOD=∠BOE,
∴$\widehat{AD}$=$\widehat{BE}$.
点评 本题考查了等腰三角形的性质,圆心角、弧、弦之间的关系,能熟练地运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
8.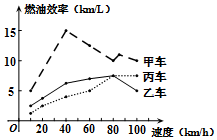 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )| A. | 当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km | |
| B. | 消耗1升汽油,丙车最多可行驶5km | |
| C. | 当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同 | |
| D. | 当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少 |
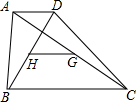 如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).
如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD). 如图,四边形ABCD中,AB∥CD,AD=CD,E、F分别是AB、BC的中点,若∠1=30°,则∠DAC=30°.
如图,四边形ABCD中,AB∥CD,AD=CD,E、F分别是AB、BC的中点,若∠1=30°,则∠DAC=30°.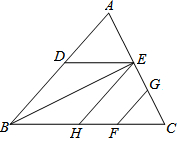 请将下列证明过程补充完整:如图,在△ABC中,DE∥BC,GF∥AB,∠ABC=∠DEH,求证:GF∥EH.
请将下列证明过程补充完整:如图,在△ABC中,DE∥BC,GF∥AB,∠ABC=∠DEH,求证:GF∥EH.