题目内容
3.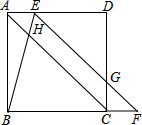 如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC; (2)求∠BEF大小.
分析 (1)根据有一组对边平行且相等的四边形是平行四边形即可判定.
(2)先确定△GCF是等腰直角三角形,得出CG=AE,然后通过△BAE≌△BCG,得出BE=BG=EG,即可求得.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD∥BF,
∵AE=CF,
∴四边形ACFE是平行四边形,
∴EF∥AC,
(2)解: 连接BG,如图所示:
连接BG,如图所示:
∵EF∥AC,
∴∠F=∠ACB=45°,
∵∠GCF=90°,
∴∠CGF=∠F=45°,
∴CG=CF,
∵AE=CF,
∴AE=CG,
在△BAE与△BCG中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠BAE=∠BCG=90°}&{\;}\\{AE=CG}&{\;}\end{array}\right.$,
∴△BAE≌△BCG(SAS)
∴BE=BG,
∵BE=EG,
∴△BEG是等边三角形,
∴∠BEF=60°.
点评 本题考查了平行四边形的判定及性质,全等三角形的判定及性质,正方形的性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
11.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数y=$\frac{kb}{x}$的图象在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第一、三象限 | D. | 第二、四象限. |
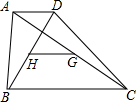 如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).
如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).
 如图,四边形ABCD中,AB∥CD,AD=CD,E、F分别是AB、BC的中点,若∠1=30°,则∠DAC=30°.
如图,四边形ABCD中,AB∥CD,AD=CD,E、F分别是AB、BC的中点,若∠1=30°,则∠DAC=30°.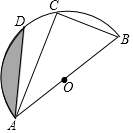 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).