题目内容
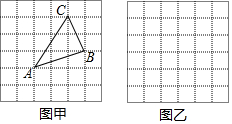
6.小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求△ABC的面积.小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.
请回答:
(1)求图1中△ABC的面积;
参考小明解决问题的方法,完成下列问题:
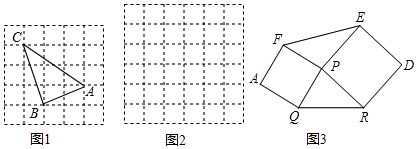
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).
①利用构图法在答题卡的图2中画出三边长分别为$\sqrt{13}$、2$\sqrt{5}$、$\sqrt{29}$的格点△DEF;
②计算△DEF的面积是8.
(3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF.若PQ=2$\sqrt{2}$,PR=$\sqrt{13}$,QR=$\sqrt{17}$,求六边形AQRDEF的面积.
分析 (1)利用网格表示出各部分面积,进而得出答案;
(2)利用勾股定理借助网格求出即可;
(3)六边形AQRDEF的面积=边长为2$\sqrt{2}$的正方形面积+边长为$\sqrt{13}$的正方形面积+△PEF的面积+△PQR的面积,其中两个三角形的面积分别用长方形的面积减去各个小三角形的面积.
解答 解:(1)△ABC的面积为:3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=3.5;
故答案为:3.5;
(2)如图所示:
① ;
;
②S△DEF=4×5-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×5=8;
故答案为:8.
(3)如图:∵S△PEF=5×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×3=5,
S△PQR=4×3-$\frac{1}{2}$×4×1-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×3=5,
∴六边形AQRDEF的面积=8+13+5+5=31.
故六边形AQRDEF的面积为31.
故答案为:31.
点评 此题主要考查了勾股定理以及三角形面积求法,利用勾股定理求出各边长是解题关键.

练习册系列答案
相关题目
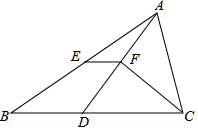 如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.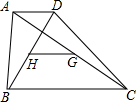 如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).
如图,在四边形ABCD中,AD∥BC,AB与CD不平行,H、G分别是两条对角线BD、AC的中点,求证:GH∥AD,且GH=$\frac{1}{2}$(BC-AD).