题目内容
10. 如图,在△ABC中,AB=AC,∠A=90°,∠ACB的平分线交AB于点D,则$\frac{AC}{AD}$的值是$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,∠ACB的平分线交AB于点D,则$\frac{AC}{AD}$的值是$\sqrt{2}$+1.
分析 作DE⊥BC于E,设AD=x,根据角平分线的性质得到DE=AD=x,根据等腰直角三角形的性质得到BD=$\sqrt{2}$x,根据题意计算即可.
解答 解: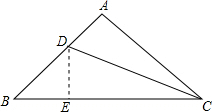 作DE⊥BC于E,
作DE⊥BC于E,
设AD=x,
∵CD是∠ACB的平分线,∠A=90°,DE⊥BC,
∴DE=AD=x,
∵AB=AC,∠A=90°,
∴∠B=45°,
∴BD=$\sqrt{2}$x,
则AC=AB=($\sqrt{2}$+1)x,
∴$\frac{AC}{AD}$=$\sqrt{2}$+1,
故答案为:$\sqrt{2}$+1.
点评 本题考查的是角平分线的性质和等腰直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各数0,$\frac{9}{7}$,$\sqrt{2}$,0.1235中无理数的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.
如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.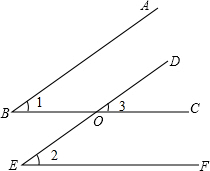 如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF.
如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF.