题目内容
8.已知线段AB=10cm,直线AB上有一点C,BC=5cm,M是线段AB上的点,且AC:BM=3:1,求线段AM的长.分析 根据线段的和差,可得AC的长,根据比例的性质,可得BM的长,再根据线段的和差,可得答案.
解答 解:①当C在线段AB的延长线上时,
如图1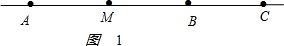 ,
,
由线段的和差,得,
AC=AB+BC=10+5=15cm,
由比例的性质,得
BM=$\frac{1}{3}$AC=$\frac{1}{3}$×15=5cm.
由线段的和差,得
AM=AB-BM=15-5cm;
②当C在线段AB上时,AC=AB-BC=10-5=5cm,
如图2 ,
,
由比例的性质,得
BM=$\frac{1}{3}$AC=$\frac{1}{3}$×5=$\frac{5}{3}$cm.
由线段的和差,得
AM=AB-BM=10-$\frac{5}{3}$=$\frac{25}{3}$cm;
综上所述:线段AM的长5cm或$\frac{25}{3}$cm.
点评 本题考查了两点间的距离,利用比例的性质得出BM的长是解题关键,要分类讨论,以防遗漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.古希腊数学家帕普斯是丢潘图是最得意的一个学生,有一天他向老师请教一个问题:有4个数,把其中每3个相加,其和分别是22,24,27,20,则这个四个数是( )
| A. | 3,8,9,10 | B. | 10,7,3,12 | C. | 9,7,4,11 | D. | 9,6,5,11 |
3.$\frac{2}{5}$xm+1yn-2与-2x2y4是同类项,则m+n=( )
| A. | 2 | B. | 4 | C. | 5 | D. | 7 |
13.2014年青奥会在中国南京举行,组委会决定在各大院校中组织一批优秀的志愿者为大赛服务,各大院校优秀学子们踊跃报名,组委会对部分报名者进行了素质考核,其中三明学生的成绩如表所示:
(1)如果根据三项的平均成绩确定人选,那么谁将被录用?请计算说明.
(2)根据实际需要,组委会若将实际英语水平、文明礼仪情况、身体素质情况测试得分按5:3:2比例确定个人的测试成绩,此时谁将被录用?请计算说明.
| 测试项目 | 测试成绩 | ||
| 学生甲 | 学生乙 | 学生丙 | |
| 交际英语水平 | 72 | 85 | 67 |
| 文明礼仪情况 | 50 | 74 | 70 |
| 身体素质情况 | 88 | 45 | 67 |
(2)根据实际需要,组委会若将实际英语水平、文明礼仪情况、身体素质情况测试得分按5:3:2比例确定个人的测试成绩,此时谁将被录用?请计算说明.
18.经过矩形ABCD顶点A、D的圆与BC边相切,圆的半径为5,AD=8,则AB=( )
| A. | 22 | B. | 8 | C. | 2或8 | D. | 4或6 |