题目内容
(本题满分10分)如图,二次函数y=-x2+nx+n2-9(n为常数)的图像经过坐标原点和x轴上另一点A,顶点在第一象限.

(1)求n的值和点A坐标;
(2)已知一次函数y=-2x+b(b >0)分别交x轴、y轴于M、N两点.点P是二次函数图像的y轴右侧部分上的一个动点,若PN⊥NM于N点,且△PMN与△OMN相似,求点P坐标.
(1)、A(3,0);(2)、P( ,
, )和P(2,2)
)和P(2,2)
【解析】
试题分析:(1)、将点(0,0)代入求出n的值,从而得到函数解析式,得出点A的坐标;(2)、首先求出M和N的坐标,然后分两种情况进行讨论得到答案.
试题解析:(1)、∵图像经过坐标原点 ∴ -9=0 ∴n=3或-3
-9=0 ∴n=3或-3
∵顶点在第一象限 ∴n=3 ∴y=- +3x ∴点A的坐标为(3,0)
+3x ∴点A的坐标为(3,0)
、过P作PB⊥y轴于B,设P(x,- +3x) ∵PN⊥MN ∠NOM=90° ∴要使△PMN与△OMN相似
+3x) ∵PN⊥MN ∠NOM=90° ∴要使△PMN与△OMN相似
则分两种情况:①、△PMN∽△MNO ②、△PMN∽△NMO
∵一次函数y=-2x+b分别交x轴、y轴于点M、N
∴OM= ON=b ∴
ON=b ∴
①、当△PMN∽△MNO(如图1),得 ∵PN⊥NM,PB⊥y轴
∵PN⊥NM,PB⊥y轴
∴△PNB∽△MNO ∴
∴x= ,x=0(舍去) ∴点P的坐标为(
,x=0(舍去) ∴点P的坐标为( ,
, )
)
②、当△PMN∽△NMO时(如图2),得: 解法同上,得x=2,x=0(舍去)
解法同上,得x=2,x=0(舍去)
∴点P的坐标为(2,2)
综上所述:满足条件的点有2个:P( ,
, )和P(2,2).
)和P(2,2).

考点:三角形相似的应用、求二次函数解析式.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目





 的
的 与
与 的部分对应值如下表:
的部分对应值如下表:
 时,
时, 的值为
的值为

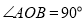 ,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴
,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴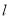 的对称点为
的对称点为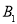 , 求点P的坐标和
, 求点P的坐标和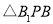 的面积.
的面积. 
 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )