题目内容
(本题满分6分)如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:(1)△ADC∽△ABE; (2)BE=CF.

略
【解析】
试题分析:根据垂直和直径所对的圆周角为直角可得∠ADC=∠ABE=90°,根据同弧所对的圆周角相等可得∠E=∠ACB,从而得到三角形相似,根据三角形相似可得∠CAD=∠BAE,从而说明BE=CF.
试题解析:(1)、∵AF⊥BC ∴∠ADC=90° ∵AE是圆的直径 ∴∠ABE=90° ∴∠ADC=∠ABE
根据同弧所对的圆周角相等可得∠E=∠ACB ∴△ADC∽△ABE
(2)、∵△ADC∽△ABE ∴∠CAD=∠BAE ∴弧BE=弧CF ∴BE=CF.
考点:三角形相似的判定,圆的基本性质.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 中,半径OD⊥弦AB于点C,连接AO并延长交
中,半径OD⊥弦AB于点C,连接AO并延长交
 B.8 C.2
B.8 C.2 D.2
D.2

 ,AE=3,求AF的长.
,AE=3,求AF的长. ,S四边形BCFE=8,则S△ABC等于
,S四边形BCFE=8,则S△ABC等于

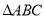 绕着点
绕着点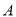 顺时针旋转
顺时针旋转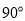 ,
,
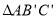 ;
; 在旋转过程中所扫过的扇形面积。
在旋转过程中所扫过的扇形面积。
