题目内容
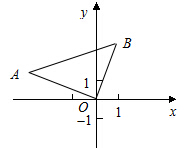
在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO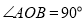 ,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴
,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴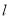 的对称点为
的对称点为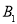 , 求点P的坐标和
, 求点P的坐标和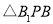 的面积.
的面积.
(1)、B(1,3);(2)、y=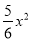 +
+ ;(3)、
;(3)、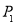
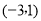 、
、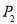
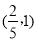 、
、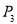
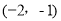 、
、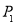
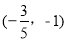
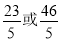
【解析】
试题分析:(1)、分别作AC⊥x轴于C,BD⊥x轴于D,证明△ACO和△BOD全等从而求出点B的坐标;(2)、利用待定系数法求出函数解析式;(3)、首先求出对称轴方程,然后根据对称的性质求出点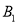 的坐标,设出点P的坐标为(k,1)和(k,-1),将P点坐标代入函数解析式求出k的值,然后计算三角形的面积.
的坐标,设出点P的坐标为(k,1)和(k,-1),将P点坐标代入函数解析式求出k的值,然后计算三角形的面积.
试题解析:(1)、作AC⊥x轴于C,作BD⊥x轴于D.
则∠ACO=∠ODB=90°, ∴∠AOC+∠OAC=90°. 又∵∠AOB=90°, ∴∠AOC+∠BOD=90°
∴∠OAC=∠BOD 又∵AO=BO ∴△ACO≌△ODB ∴OD=AC=1 DB=OC=3 ∴点B的坐标为(1,3).
(2)、因为抛物线过原点,故可设所求抛物线的解析式为: .将
.将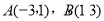 两点代入,得
两点代入,得
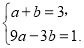 解得
解得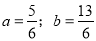 . 故所求抛物线的解析式为
. 故所求抛物线的解析式为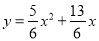 .
.
(3)、在抛物线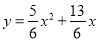 中,对称轴
中,对称轴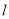 的方程是
的方程是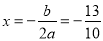 .
.
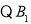 是
是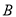 关于抛物线的对称轴
关于抛物线的对称轴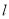 的对称点,故
的对称点,故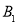 坐标
坐标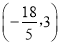 ,
, 
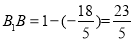
由题意,设抛物线上到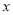 轴的距离为1的点为
轴的距离为1的点为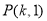 或
或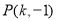 ,则
,则
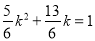 或
或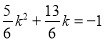 即:
即: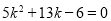 或
或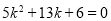
解得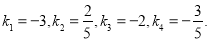
即抛物线上到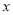 轴的距离为1的点为:
轴的距离为1的点为: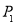
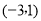 、
、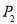
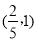 、
、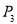
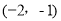 、
、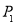
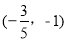 .
.
在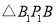 中,底边
中,底边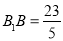 ,高的长为2,故
,高的长为2,故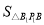
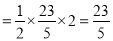 ,
,
同理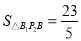 ,
,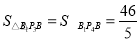
考点:二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


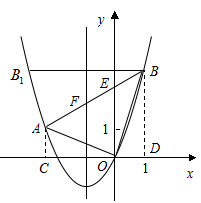
 B.
B. C.
C. D.
D.
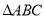 绕着点
绕着点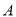 顺时针旋转
顺时针旋转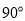 ,
,
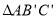 ;
;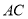 在旋转过程中所扫过的扇形面积。
在旋转过程中所扫过的扇形面积。