题目内容
20．
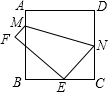如图，将长为8cm的正方形纸片折叠，使点D落在BC边中点E处，点A落在F处，折痕为MN，则线段CN的长为（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |
分析 根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8-x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．
解答 解：由题意设CN=x cm，则EN=（8-x）cm，
又∵CE=$\frac{1}{2}$DC=4cm，
∴在Rt△ECN中，EN2=EC2+CN2，即（8-x）2=42+x2，
解得：x=3，即CN=3cm．
故答案为：3cm．
点评 本题考查翻折变换的问题，折叠问题其实质是轴对称，对应线段相等，对应角相等，找到相应的直角三角形利用勾股定理求解是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，∠ABC=90°，AB=12，BC=5，若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（ ）
11．下列命题中的真命题是（ ）
| A． | 经过一点有且只有一条直线与已知直线平行 | |
| B． | 任何一个角都有一个余角和一个补角 | |
| C． | 同位角相等 | |
| D． | 互补的两个角不能都大于90° |
如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，∠DOB=2∠EOD，求∠AOC，∠COB的度数．
15．下面四个二次根式，化简后可以与$\sqrt{3}$进行合并的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{18}$ | C． | $\sqrt{\frac{3}{2}}$ | D． | $\sqrt{12}$ |
5．
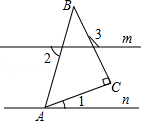如图，直线m∥n，点A在直线n上，∠C=90°，∠1=25°，∠2=70°，则∠3的度数为（ ）
如图，直线m∥n，点A在直线n上，∠C=90°，∠1=25°，∠2=70°，则∠3的度数为（ ）| A． | 105° | B． | 110° | C． | 115° | D． | 120° |
9．两条平行线被第三条直线所截，两组内错角的平分线相交所成的四边形是（ ）
| A． | 正方形 | B． | 菱形 | C． | 矩形 | D． | 梯形 |