题目内容
9.两条平行线被第三条直线所截,两组内错角的平分线相交所成的四边形是( )| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 梯形 |
分析 这两组内错角,其实可以看作两组同旁内角.同旁内角的角平分线的夹角为90度,又证得邻补角的角平分线的夹角为90度,因而得证两组内错角的平分线相交所成的四边形是矩形.
解答 解:已知直线AB∥CD,EF分别与AB,CD相交于E,F
两组内错角的平分线分别相交于M,N
则有∠MEF=$\frac{1}{2}$∠AEF,∠NFE=$\frac{1}{2}$∠DFE
∵AB∥CD,则∠AEF=∠DFE
∴∠MEF=∠NFE
即EM∥FN
同理FM∥EN
∴四边形EMFN为平行四边形
∠MEN=∠MEF+∠NEF=$\frac{1}{2}$∠AEF+$\frac{1}{2}$∠BEF=$\frac{1}{2}$(∠AEF+∠BEF)=$\frac{1}{2}$×180°=90°
∵平行四边形有一个内角为90°
∴四边形EMFN为矩形.
故选C.
点评 本题考查了矩形的判定,正确运用有一个角是直角的平行四边形是矩形,是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
19.下列图形中,∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
20.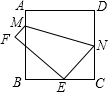 如图,将长为8cm的正方形纸片折叠,使点D落在BC边中点E处,点A落在F处,折痕为MN,则线段CN的长为( )
如图,将长为8cm的正方形纸片折叠,使点D落在BC边中点E处,点A落在F处,折痕为MN,则线段CN的长为( )
 如图,将长为8cm的正方形纸片折叠,使点D落在BC边中点E处,点A落在F处,折痕为MN,则线段CN的长为( )
如图,将长为8cm的正方形纸片折叠,使点D落在BC边中点E处,点A落在F处,折痕为MN,则线段CN的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
17.小明和小李两位同学这学期数学六次测试的平均成绩恰好都是85分,方差分别为S小明2=1.5,S小李2=2,则成绩最稳定的是( )
| A. | 小明 | B. | 小李 | C. | 小明和小李 | D. | 无法确定 |
4.设n为正整数,且n<$\sqrt{62}$<n+1,则n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
14.下列调查,合适采用全面调查方式的是( )
| A. | 检测某型号手机的抗摔情况 | |
| B. | 了解某校七(1)班全体同学的身高情况 | |
| C. | 检测一批农产品的农药残留情况 | |
| D. | 检测某试验区水稻的株高生长情况 |
18.在实数-$\frac{22}{7}$、$\sqrt{9}$、π、$\root{3}{8}$中,是无理数的是( )
| A. | -$\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | π | D. | $\root{3}{8}$ |
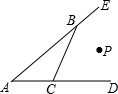 如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是①②③④.(填序号)
如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是①②③④.(填序号)