题目内容
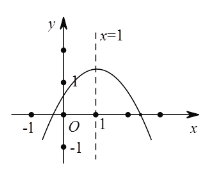
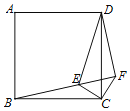
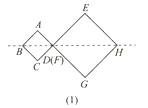
【题目】如图所示,四边形ABCD是边长为1的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B、D(F)、H在同一条直线上.将正方形ABCD沿F→H方向平移到点B与点H重合时停止.设点D,F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与x之间函数关系的图像是( ).


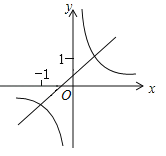
A. 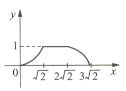 B.
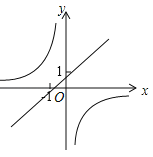
B. 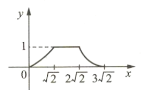 C.
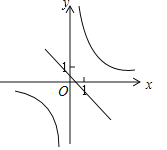
C. 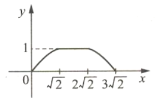 D.
D. 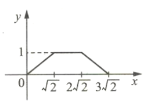
【答案】B
【解析】
正方形ABCD与正方形EFGH重叠部分主要分为3个部分,属于分段函数;通过列出每一段的函数关系式,得到每一段的函数图象,从而选出正确答案的.
由DF=x,正方形ABCD与正方形EFGH重叠部分的面积为y.则
①y=![]() DF2=
DF2=![]() x2(0≤x<
x2(0≤x<![]() );
);
②y=1(![]() ≤x<
≤x<![]() );
);
③∵BH=3![]() -x
-x
∴y=![]() BH2=
BH2=![]() x2-3
x2-3![]() x+9(2
x+9(2![]() ≤x<3
≤x<3![]() ).
).
综上可知,图象是

故选B.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目