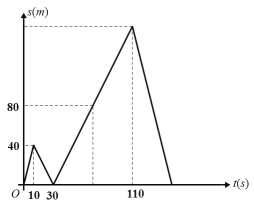
题目内容
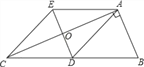
【题目】如图所示,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为lcm/s.连接PQ,设运动时间为t(s)(0<t<4).

(1)当t为何值时,PQ⊥AC?
(2)设△APQ的面积为S,求S与t的函数关系式,并求出当t为何值时,S取得最大值?S的最大值是多少?
【答案】(1)t为![]() 时,PQ⊥AC;(2)t=
时,PQ⊥AC;(2)t=![]() ,S有最大值,最大值为
,S有最大值,最大值为![]() .
.
【解析】
(1)先根据勾股定理求得AB=5,再因为∠ACB=90°,所以当PQ⊥AC时,PQ∥BC,从而得出![]() ,由运动知,BP=t,得出AP=5-t,AQ=t,代入前面比例式建立方程即可得出结论;
,由运动知,BP=t,得出AP=5-t,AQ=t,代入前面比例式建立方程即可得出结论;
(2)过点P作PH⊥AC于H,由△APH∽△ABC,得出![]() =
=![]() ,从而求出AB,再根据
,从而求出AB,再根据![]() =
=![]() ,,得出PH=3-
,,得出PH=3-![]() t,则△AQP的面积为:
t,则△AQP的面积为:![]() AQPH=
AQPH=![]() t(3-
t(3-![]() t),最后进行整理即可得出答案;
t),最后进行整理即可得出答案;
(1)∵PQ⊥AC,
∴∠AQP=∠C=90°,
∴PQ∥BC,
∴![]() =
=![]() ,
,
在Rt△ACB中,AB=![]() =
=![]() =5,
=5,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
∴t为![]() 时,PQ⊥AC.
时,PQ⊥AC.
(2)如图,作PH⊥AC于H.
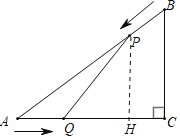
∵PH∥
∴△APH∽△ABC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PH=![]() (5﹣t),
(5﹣t),
∴S=![]() AQPH=
AQPH=![]() t
t![]() (5﹣t)=﹣
(5﹣t)=﹣![]() t2+
t2+![]() t=﹣
t=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴t=![]() ,S有最大值,最大值为
,S有最大值,最大值为![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目