题目内容
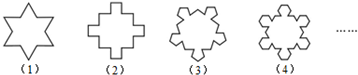
如图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,…,依此类推,由正n边形“扩展”而来的多边形的边数记为an(n≥3).则a7的值是 ,当
+
+
+…+
的结果是
时,n的值为 .
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| an |
| 197 |
| 600 |

考点:规律型:图形的变化类
专题:
分析:结合图形观察数字,发现:a3=12=3×4,a4=20=4×5,进一步得到an=n(n+1),代入求得a7的值;在计算
+
+
+…+
的时候,拆分进行简便计算.
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| an |
解答:
解:观察图形可得:an=n(n+1);
a7=7×8=56,
当
+
+
+…+
=
时,
+
+
+…+
=
-
+
-
+
-
+…+
-
=
-
=
解得:n=199.
故答案为:56,199.
a7=7×8=56,
当
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| an |
| 197 |
| 600 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 1 |
| n(n+1) |
| 197 |
| 600 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n |
| 1 |
| n+1 |
| 197 |
| 600 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 197 |
| 600 |
解得:n=199.
故答案为:56,199.
点评:此题考查了图形的变化规律题,注意从特殊推广到一般,解方程时能够利用分数的加减法进行简便计算.

练习册系列答案
相关题目
将抛物线y=x2先向右平移2个单位,再向下平移3个单位,那么得到的新的抛物线的解析式是( )
| A、y=(x+2)2+3 |
| B、y=(x+2)2-3 |
| C、y=(x-2)2+3 |
| D、y=(x-2)2-3 |
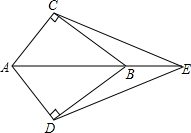 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD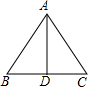 如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是
如图,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,其根据是 在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.
在如图所示的一张零件图中,已知AD=73mm,BD=69mm,CD=17mm,求AB和BC的长.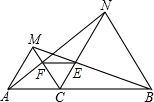 如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形. 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数.
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数.