题目内容
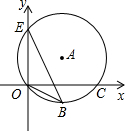 如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=
如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=考点:圆周角定理,坐标与图形性质
专题:
分析:首先连接EC,由点E(0,3),O(0,0),C(5,0)在⊙A上,可求得OE,OC,EC的长,继而求得cos∠OCE的值,又由圆周角定理,可得∠OBE=∠OCE,即可求得答案.
解答: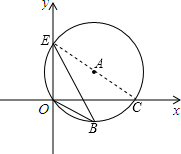 解:连接EC,
解:连接EC,
∵点E(0,3),O(0,0),C(5,0)在⊙A上,
∴OE=3,OC=5,
∵∠EOC=90°,
∴EC=
=
,
∴cos∠OCE=
=
,
∵∠OBE=∠OCE,
∴cos∠OBE=
.
故答案为:
.
 解:连接EC,
解:连接EC,∵点E(0,3),O(0,0),C(5,0)在⊙A上,
∴OE=3,OC=5,
∵∠EOC=90°,
∴EC=
| 32+52 |
| 34 |
∴cos∠OCE=
| 5 | ||
|
5
| ||
| 34 |
∵∠OBE=∠OCE,
∴cos∠OBE=
5
| ||
| 34 |
故答案为:
5
| ||
| 34 |
点评:本题重点考查了同弧所对的圆周角相等及解直角三角形的知识.注意锐角三角函数的概念:在直角三角形中,正弦等于对比斜;余弦等于邻比斜;正切等于对比邻.

练习册系列答案
相关题目
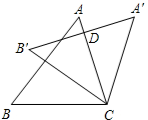 如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )
如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )| A、35° | B、65° |
| C、55° | D、25° |
(m+n)(m+n-2)-8=0,则m+n的值是( )
| A、4 | B、-2 |
| C、4或-2 | D、-4或2 |
一元二次方程2x2-2=4x的一次项系数为( )
| A、4 | B、-4 | C、4x | D、-4x |
若a=56,b=65,那么3030用a,b来表示为( )
| A、ab |
| B、a3b4 |
| C、a5b6 |
| D、(ab)6 |
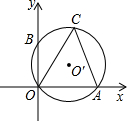 如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )
如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( ) 如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=120°,∠C=40°,则∠DAE的度数是
如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=120°,∠C=40°,则∠DAE的度数是 【材料阅读】:我们知道,当一条直线与一个圆有0个、1个、两个公共点时,分别称这条直线与这个圆相离、相切、相交,类似地,我们定义:当一条直线与一个正方形没有交点时,称这条直线与正方形相离;当一条直线与一个正方形只有一个公共点时,称这条直线与正方形相切,当一条直线与正方形有两个公共点时,称这条直线与这个正方形相交.
【材料阅读】:我们知道,当一条直线与一个圆有0个、1个、两个公共点时,分别称这条直线与这个圆相离、相切、相交,类似地,我们定义:当一条直线与一个正方形没有交点时,称这条直线与正方形相离;当一条直线与一个正方形只有一个公共点时,称这条直线与正方形相切,当一条直线与正方形有两个公共点时,称这条直线与这个正方形相交.