题目内容
 【材料阅读】:我们知道,当一条直线与一个圆有0个、1个、两个公共点时,分别称这条直线与这个圆相离、相切、相交,类似地,我们定义:当一条直线与一个正方形没有交点时,称这条直线与正方形相离;当一条直线与一个正方形只有一个公共点时,称这条直线与正方形相切,当一条直线与正方形有两个公共点时,称这条直线与这个正方形相交.
【材料阅读】:我们知道,当一条直线与一个圆有0个、1个、两个公共点时,分别称这条直线与这个圆相离、相切、相交,类似地,我们定义:当一条直线与一个正方形没有交点时,称这条直线与正方形相离;当一条直线与一个正方形只有一个公共点时,称这条直线与正方形相切,当一条直线与正方形有两个公共点时,称这条直线与这个正方形相交.【问题解决】:如图,在平面直角坐标系中,正方形ABCD的顶点A,D在x轴上,且A(2,0)、D(4,0).
(1)判断直线y=-x+3与正方形ABCD的位置关系是
(2)若直线y=2x+a与正方形ABCD相切,则a的值=
(3)如图,直线l的解析式为y=-
| 3 |
考点:一次函数综合题
专题:
分析:(1)由A(2,0)、D(4,0)可以求出AD=2,由正方形的性质可以得出AD=CD=BC=AB=2,可以得出C、B的坐标.当x=2或y=0时求出对应的y的值及x的值就可以求出直线与正方形的交点坐标而得出结论;
(2)由直线y=2x+a可得出直线是升函数.且子线与正方形相切,得出直线经过D点和B点,将B、D的坐标代入解析式就可以求出结论;
(3)由直线y=-
x+b与正方形DABC相交,直线是降函数就可以得出当直线过点A或点C时求出a的值,就可以求出直线与x轴和y轴的交点坐标,由勾股定理求出AE和FG的值,作ON⊥FG交AE于点M,求出OM,ON的值即可.
(2)由直线y=2x+a可得出直线是升函数.且子线与正方形相切,得出直线经过D点和B点,将B、D的坐标代入解析式就可以求出结论;
(3)由直线y=-
| 3 |
解答:解:(1)如图1,由题意,得
∵A(2,0)、D(4,0),
∴AD=2.
∵四边形ABCD是正方形,
∴AD=CD=BC=AB=2,
∴B(2,2),C(4,2).
当x=2时,y=1,
当y=0时,x=3.
∴直线l与x轴交于(3,0),与y轴交于(2,1),
∴直线y=-x+3与正方形ABCD相交.
故答案为:相交;
(2)如图2,由题意,得
∵直线y=2x+a与正方形ABCD相切,
∴直线y=2x+a经过点B和点D.
当直线经过点B时,0=4×2+a,a=-8,
当直线经过点D时,2=2×2+a,a=-2.
故答案为:-2或-8;
(3)如图3,∵直线y=-
x+b,
∴直线是降函数,
当直线经过点A时,0=-2
+b,b=2
∴y=-
x+2
当x=0时,y=2
,
当y=0时,x=2.
∴OE=2
,OA=2,
∴AE=4,
当直线经过点C时,2=-4
+b,b=2+4
,
∴y=-
x+2+4
,
当x=0时,y=2+4
,
当y=0时,x=
.
∴OF=2+4
,OG=
,
∴FG=
.
作ON⊥FG交AE于点M.
∴ON⊥AE.
∴
=
,
=
∴OM=
,ON=1=2
.
∴
<d<1+2
.
∴d的取值范围是:
<d<1+2
.

∵A(2,0)、D(4,0),
∴AD=2.
∵四边形ABCD是正方形,
∴AD=CD=BC=AB=2,
∴B(2,2),C(4,2).
当x=2时,y=1,
当y=0时,x=3.

∴直线l与x轴交于(3,0),与y轴交于(2,1),
∴直线y=-x+3与正方形ABCD相交.
故答案为:相交;
(2)如图2,由题意,得
∵直线y=2x+a与正方形ABCD相切,
∴直线y=2x+a经过点B和点D.
当直线经过点B时,0=4×2+a,a=-8,
当直线经过点D时,2=2×2+a,a=-2.
故答案为:-2或-8;
(3)如图3,∵直线y=-
| 3 |

∴直线是降函数,
当直线经过点A时,0=-2
| 3 |
| 3 |
∴y=-
| 3 |
| 3 |
当x=0时,y=2
| 3 |
当y=0时,x=2.
∴OE=2
| 3 |
∴AE=4,
当直线经过点C时,2=-4
| 3 |
| 3 |
∴y=-
| 3 |
| 3 |
当x=0时,y=2+4
| 3 |
当y=0时,x=
2
| ||
| 3 |
∴OF=2+4
| 3 |
2
| ||
| 3 |
∴FG=
4
| ||
| 3 |
作ON⊥FG交AE于点M.
∴ON⊥AE.
∴
2×2
| ||
| 2 |
| 4OM |
| 2 |
(2+4
| ||||||
| 2 |
| ||||
| 2 |
∴OM=
| 3 |
| 3 |
∴
| 3 |
| 3 |
∴d的取值范围是:
| 3 |
| 3 |
点评:本题考查了直线与正方形的位置关系的运用,一次函数的解析式的运用,勾股定理的运用,三角形的面积公式的运用,正方形的性质的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
相关题目
下列合并同类项,正确的是( )
| A、2a+b=2ab |
| B、2a-a=2 |
| C、3a2+2a2=5a4 |
| D、2a2b-a2b=a2b |
若2xy2m+6z-2x2y+4yz+1是六次四项式,则m的值为( )
| A、-2 | ||
| B、-1 | ||
C、-
| ||
| D、7 |
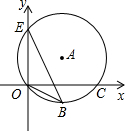 如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=
如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE= 如图,已知EF是梯形ABCD的中位线,△AEF的面积为4cm2,则梯形ABCD的面积为
如图,已知EF是梯形ABCD的中位线,△AEF的面积为4cm2,则梯形ABCD的面积为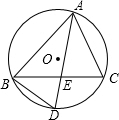 如图,△ABC内接于⊙O,I为△ABC的角的平分线交点,延长AI分别交⊙O、BC于D、E两点.
如图,△ABC内接于⊙O,I为△ABC的角的平分线交点,延长AI分别交⊙O、BC于D、E两点.