题目内容
 如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=120°,∠C=40°,则∠DAE的度数是
如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=120°,∠C=40°,则∠DAE的度数是考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据三角形内角和定理求出∠DAC,根据角平分线定义求出∠EAC,即可得出答案.
解答:解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=40°,
∴∠DAC=50°,
∵AE是△ABC的角平分线,∠BAC=120°,
∴∠EAC=
∠BAC=60°,
∴∠EAD=∠EAC-∠DAC=10°,
故答案为:10°.
∴∠ADC=90°,
∵∠C=40°,
∴∠DAC=50°,
∵AE是△ABC的角平分线,∠BAC=120°,
∴∠EAC=
| 1 |
| 2 |
∴∠EAD=∠EAC-∠DAC=10°,
故答案为:10°.
点评:本题考查了三角形内角和定理,角平分线定义的应用,解此题的关键是求出∠DAC和∠EAC的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
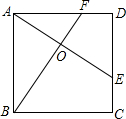 如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )
如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( ) ①AE⊥BF;②AE=BF;③S△AOB=S四边形OEDF;④BO=OF.
| A、1个 | B、2个 | C、3个 | D、4个 |
12的算术平方根介于( )
| A、5和4之间 |
| B、4与3之间 |
| C、3与2之间 |
| D、2与1之间 |
下列等式中,正确的是( )
| A、|-4|=-|4| |
| B、-52=(-5)2 |
| C、-33=(-3)3 |
| D、-|-5|=-(-5) |
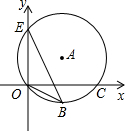 如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=
如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦,则cos∠OBE=